课程来源：GAMES101-现代计算机图形学入门-闫令琪 Lecture12
Lingqi Yan
UC Santa Barbara

网格操作：几何图形处理

• Mesh subdivision 网格细分
• Mesh simplification 网格简化
• Mesh regularization 网格正规化

细分

三角形网格的通用细分：

首先，创建更多的三角形（顶点）其次，调整它们的位置

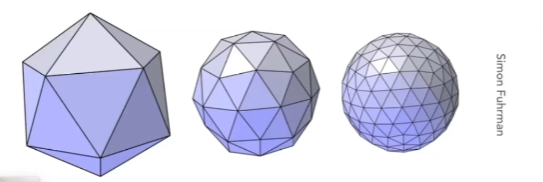
Loop细分

Loop细分和循环没有任何关系，因为发明这个细分方法的人的family name为Loop。

Loop细分-产生新的三角形

• 把每个三角形分成四个
  
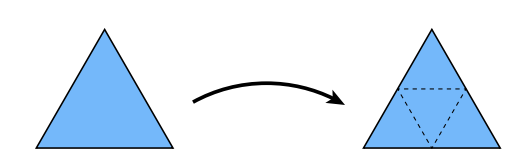
• 根据权重分配新的顶点位置
• 新/旧顶点更新的方式更新
  

Loop细分-更新

对于新的顶点：一个简单的加权平均
A和B对白点的“贡献”大一点，权重就大一点，C和D离白点远，权重就小一点。

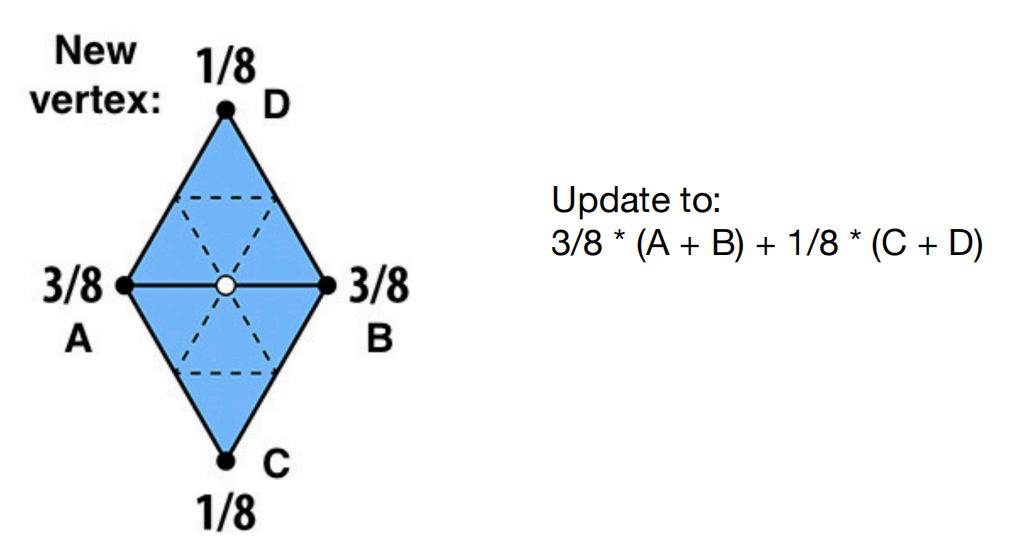
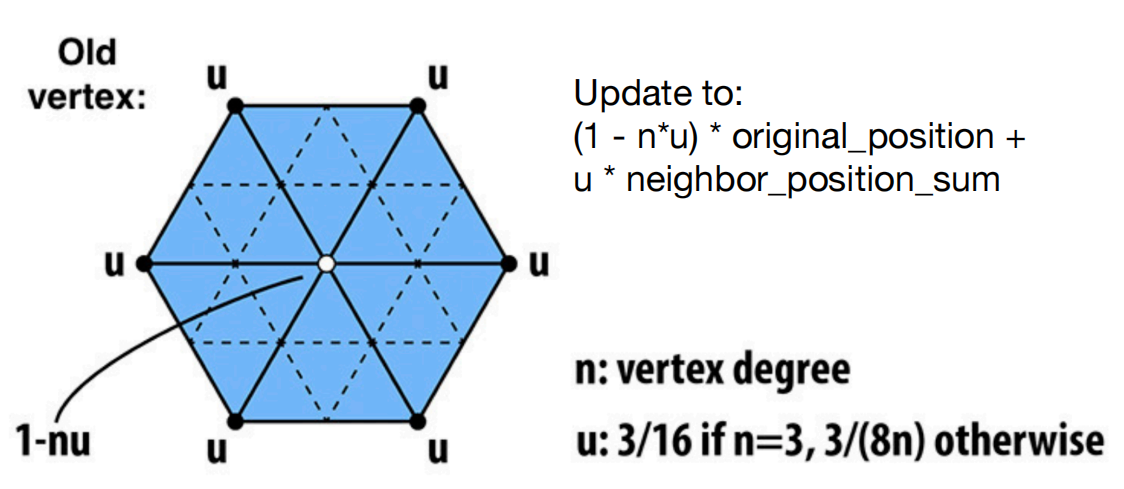
• 对于旧的顶点如何做位置的更新
  

Loop细分结果

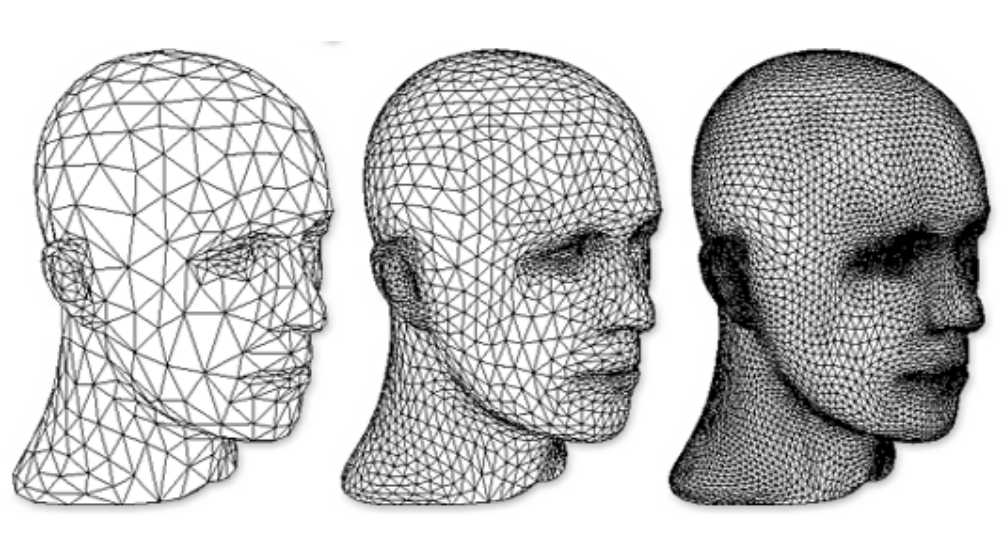
• Loop细分：先将一个三角形分成4个，再对旧的点调整位置。

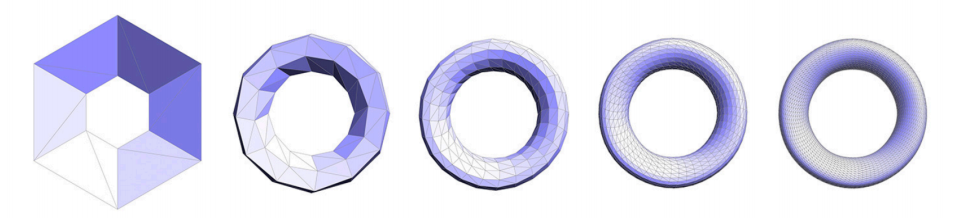
Catmull-Clark 细分

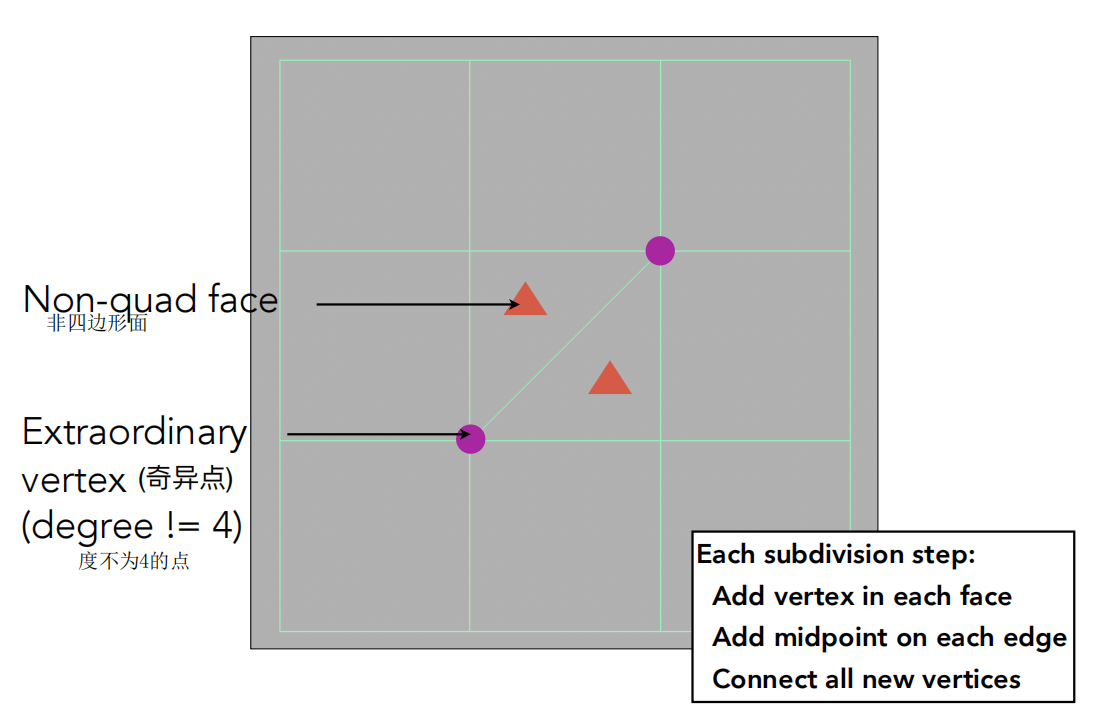
度：一个点连接的边数

• 每个细分步骤：
• 在每个面中添加顶点
• 在每条边上添加中点
• 连接所有新顶点

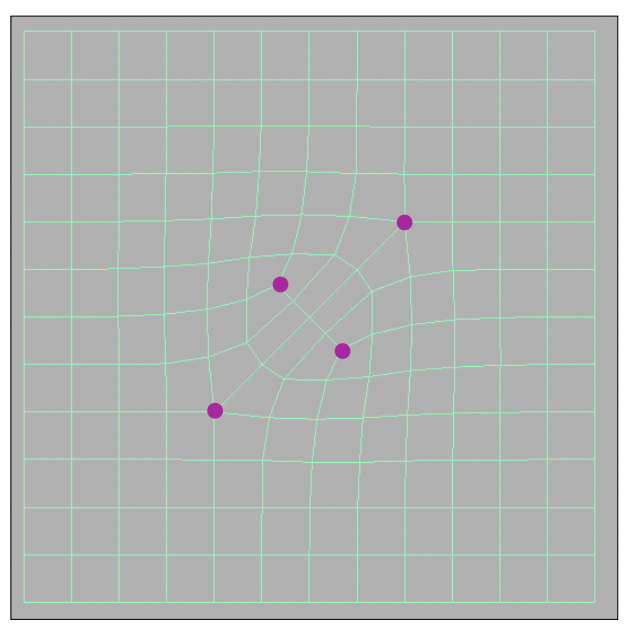
经过一次细分后，还有多少奇异点呢

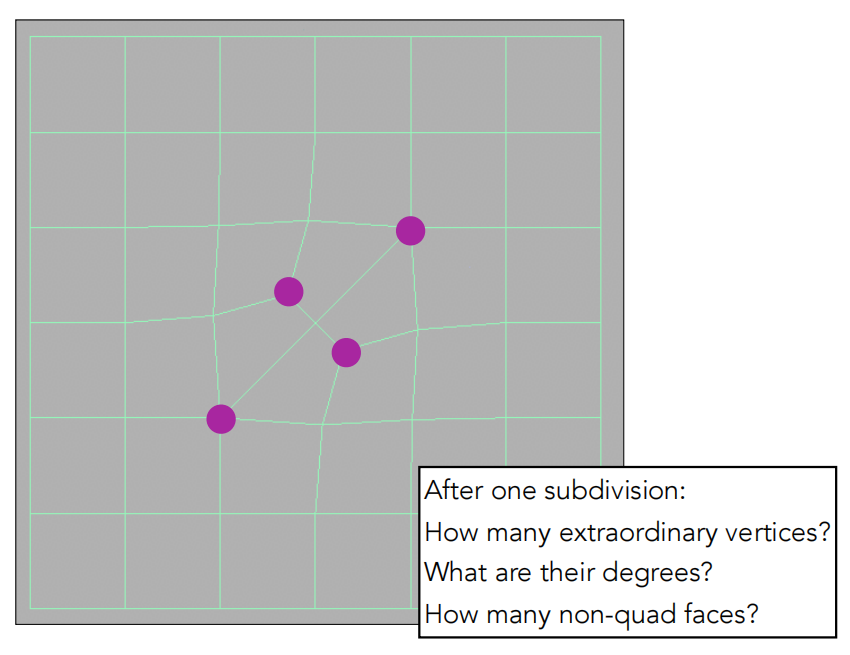
在非四边形面引入了2个新的顶点之后，奇异点的数量变为了4个。
每一个非四边形面在引入一个奇异点之后消失。
可以理解为，非四边形面经过一次Catmull-Clark 细分操作后，变成了一个奇异点。
也就是说再接着细分，奇异点的个数不会再增加了。

Catmull-Clark 细分规则

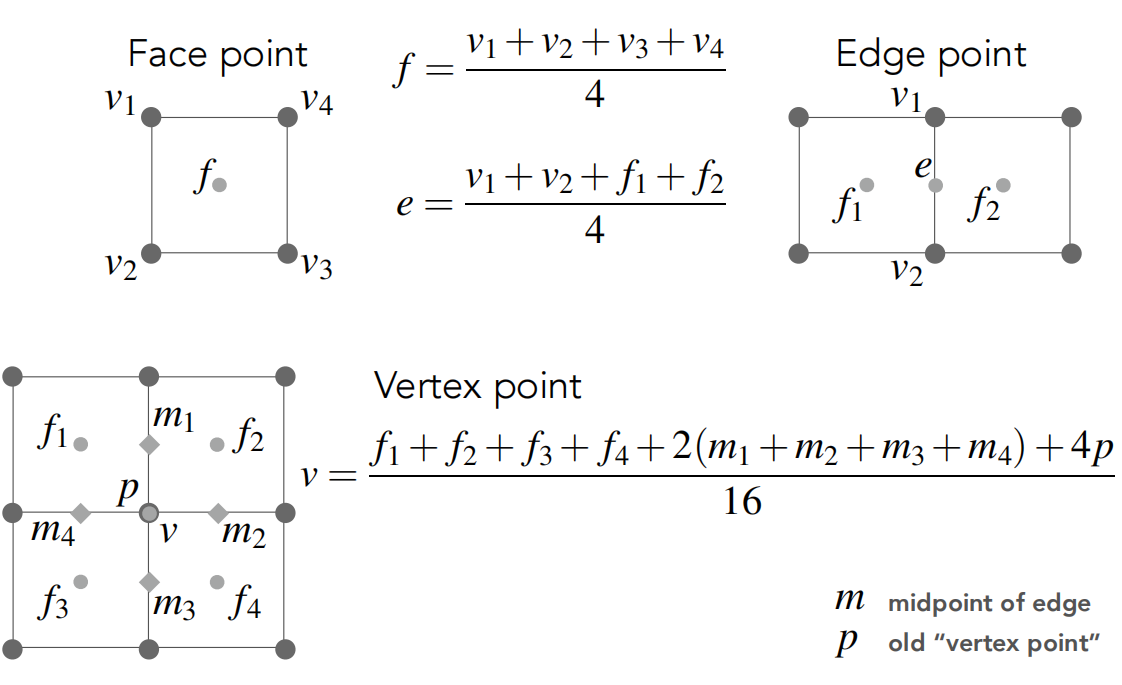
本质上来讲，和图像的模糊操作没有太大区别，以平均的方式来细分面。

Loop细分和Catmull-Clark 细分区别

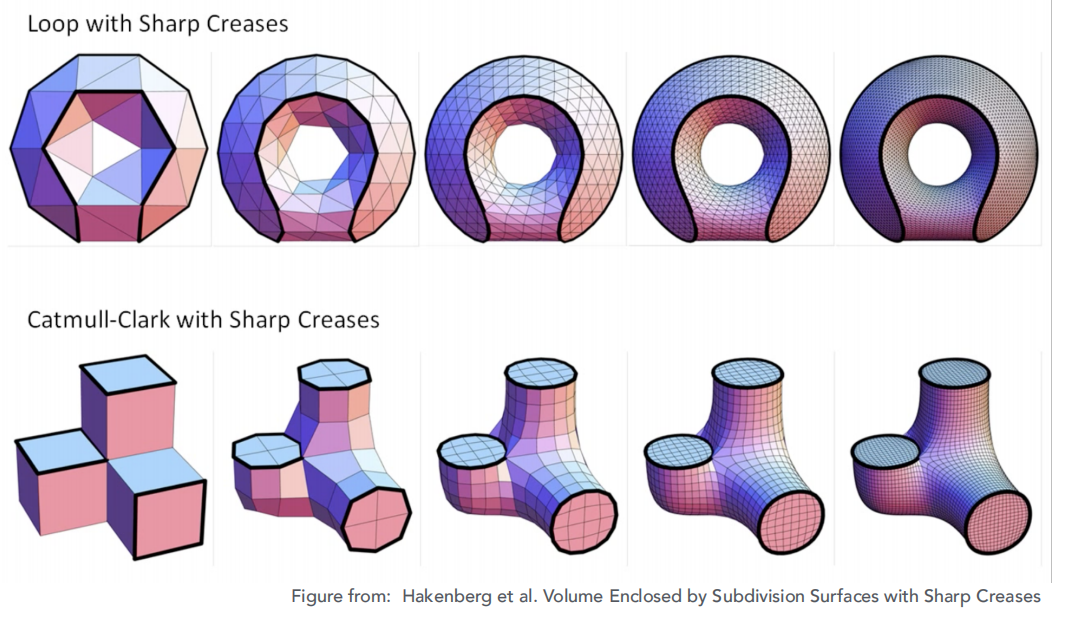
和Loop细分不同，Catmull-Clark 细分可以用于多边形面，而Loop细分只能用作三角形面。

最早的曲面细分动画

(Pixar’s “Geri’s Game”)

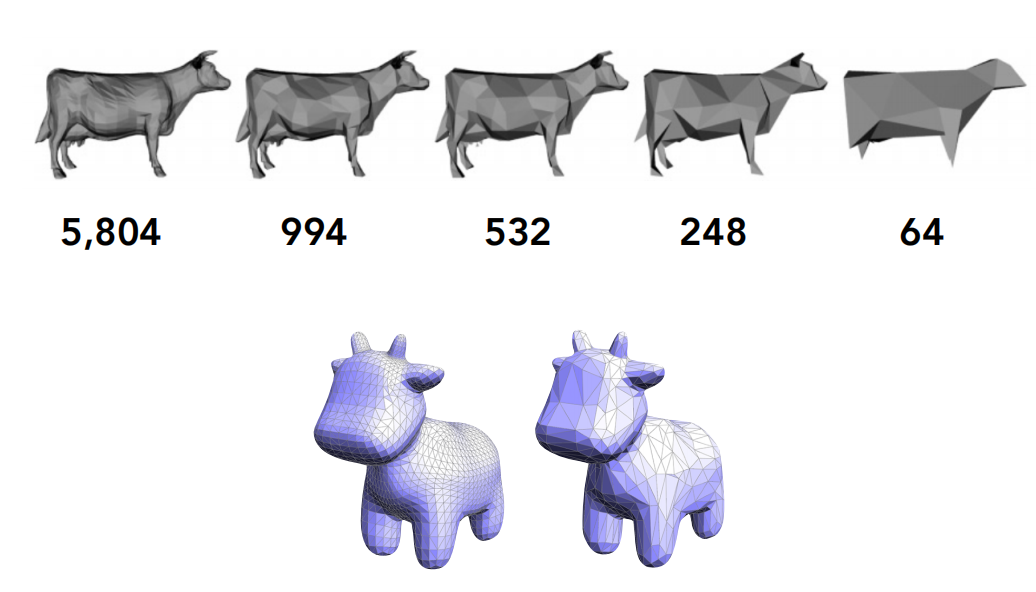
网格简化

目标：在减少网格元素的数量的同时，保持整体形状

边坍缩

假设我们使用边坍缩来简化一个网格

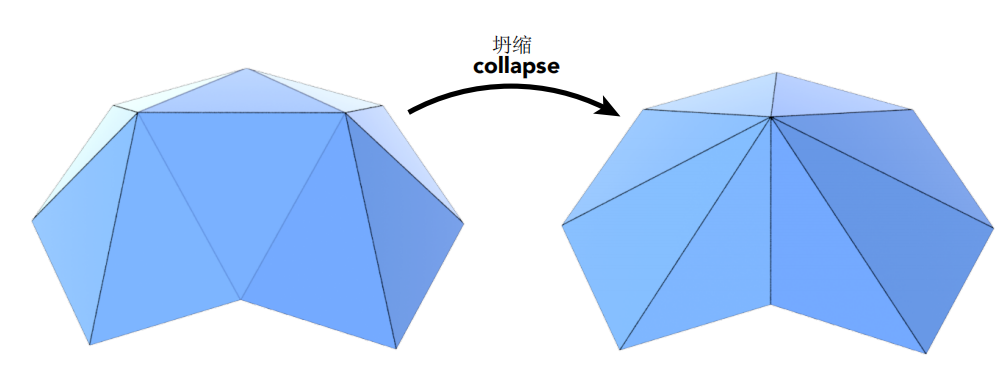
二次误差度量

引入一种误差的度量，将这个点放在某个位置，可以最小化二次误差。

二次误差：新顶点应与先前相关的三角形平面的平方距离之和最小。

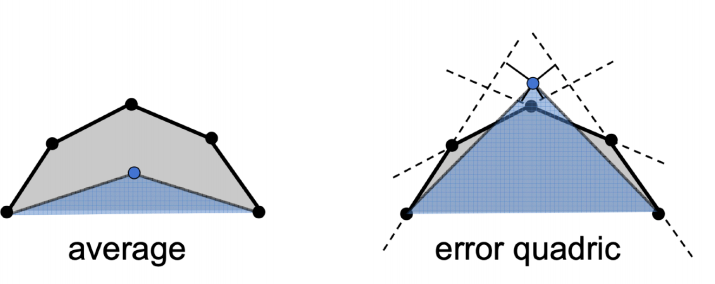
坍缩任意一条边之后，调整形成的一个顶点的位置，造成最小的二次误差。

对于每一条边，假设如果我们去坍缩他，会造成多大的二次误差。可想到一个算法，对于一个模型，我们选择二次度量误差最低的边先开始坍缩，然后坍缩第二小的，依次。

先给每一条边都打上一个分数，这个分数就是二次度量误差，然后从最小的一个开始坍缩。

但是这么做有一个问题，坍缩一条边之后，有一些边要跟着这条边坍缩，那么其他边的二次度量误差就变了。

方法：第一：从一堆边中取二次度量误差最小的边；第二：当取完最小的边坍缩完后，对其他受影响的边进行二次度量误差的更新。

这个数据结构就是优先队列，或者是堆。

这种方式是一个典型的贪心算法。

二次度量误差的实际操作