当前位置： 首页 > news >正文

【小嘟陪你刷题10】二叉树的基础面试题

news 来源：原创 2024/11/18 16:23:32

目录

  • 前言
  • 一、相同的树
    • 1.1 题解
      • 方法：深度优先搜索
    • 1.2 代码实现
  • 二、另一颗树的子树
    • 2.1 题解
      • 方法：深度优先搜索暴力匹配
    • 2.2 代码实现
  • 三、二叉树的最大深度
    • 3.1 题解
      • 方法：深度优先搜索
    • 3.2 代码实现
  • 四、二叉树的前序遍历
    • 4.1 题解
      • 方法：递归
    • 4.2 代码实现
  • 五、二叉树的中序遍历
    • 5.1 题解
      • 方法：递归
    • 5.2 代码实现
  • 六、二叉树的后序遍历
    • 6.1 题解
      • 方法：递归
    • 6.2 代码实现
  • 七、平衡二叉树
    • 7.1 题解
      • 方法一：自顶向下递归
      • 方法二：自低向上递归
    • 7.2 代码实现
      • 方法一：
      • 方法二：
  • 八、对称二叉树
    • 8.1 题解
      • 方法：递归
    • 8.2 代码实现

前言

此篇是对二叉树的练习，一些比较基础的题！

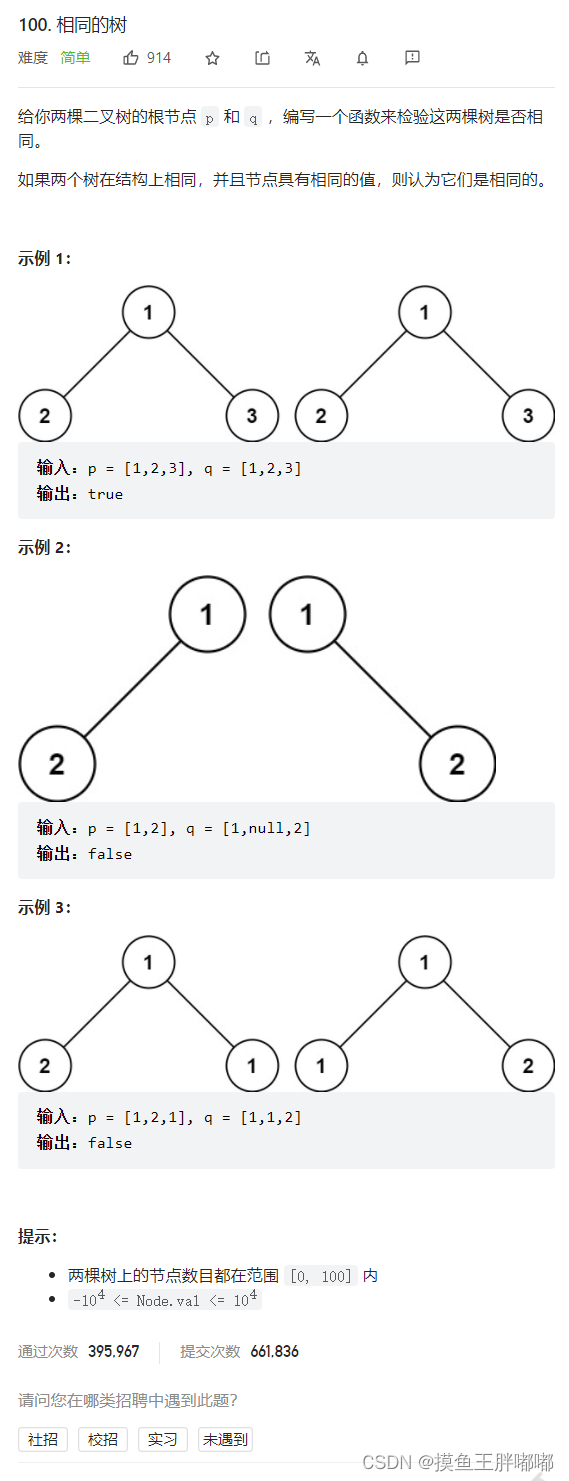
一、相同的树

在这里插入图片描述

1.1 题解

方法：深度优先搜索

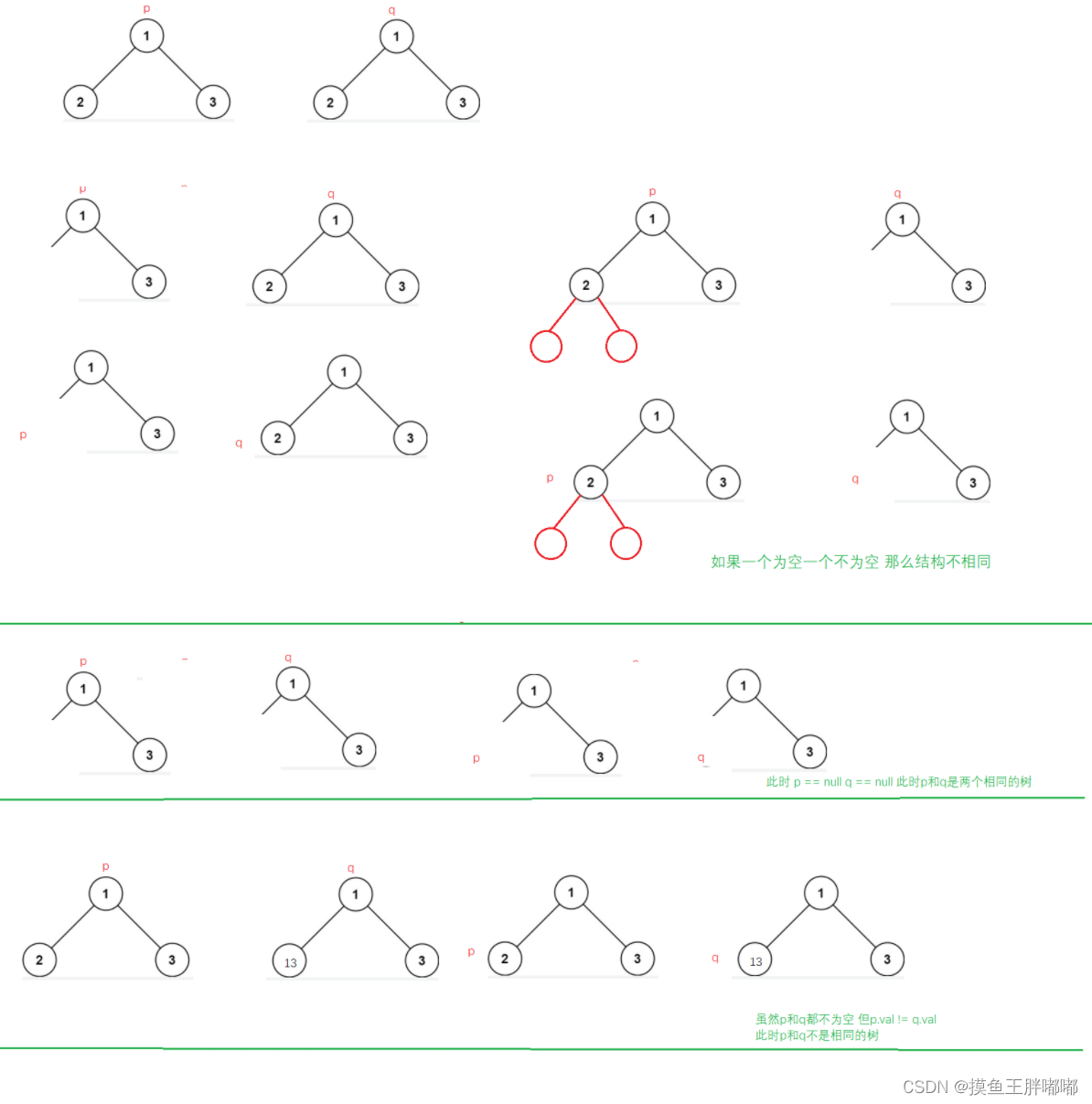
如果两个二叉树都为空，则两个二叉树相同。如果两个二叉树中有且只有一个为空，则两个二叉树一定不相同。

如果两个二叉树都不为空，那么首先判断它们的根节点的值是否相同，若不相同则两个二叉树一定不同，若相同，再分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程，因此可以使用深度优先搜索，递归地判断两个二叉树是否相同。

在这里插入图片描述

1.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q != null  || p != null && q == null ) {
            return false;
        }
        if(p == null && q == null) {
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    
    }
}

在这里插入图片描述

二、另一颗树的子树

在这里插入图片描述

2.1 题解

方法：深度优先搜索暴力匹配

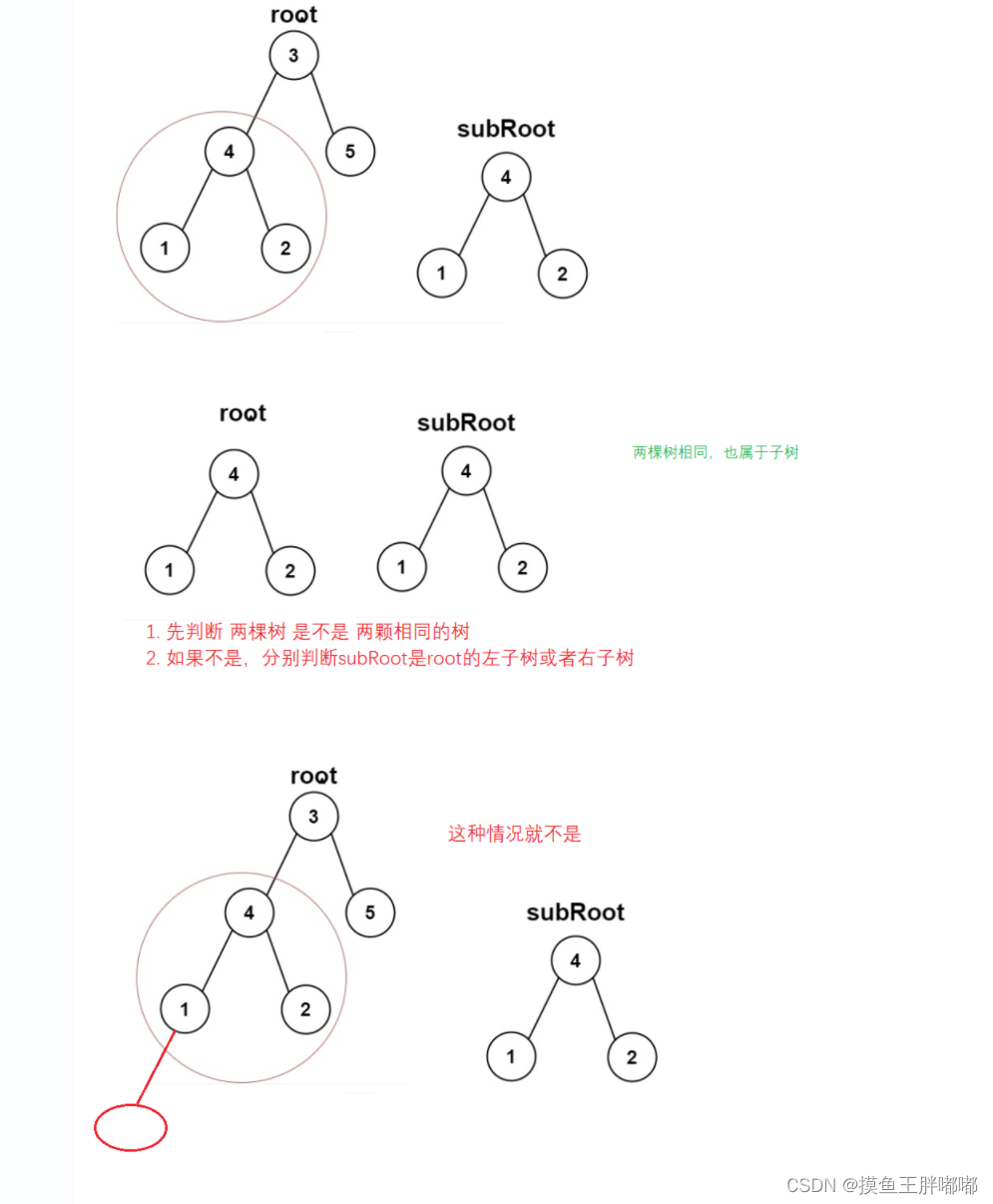
先判断二者是否为空，都为空返回false。子树可能是父树的左子树或右子树，如果都不满足返回false。
在这里插入图片描述

2.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q != null  || p != null && q == null ) {
            return false;
        }
        if(p == null && q == null) {
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    
    }
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null || subRoot == null) {
            return false;
        }
        if (isSameTree(root, subRoot)) {
            return true;
        }
        if (isSubtree(root.left, subRoot)) {
            return true;
        }
        if (isSubtree(root.right, subRoot)) {
            return true;
        }
        return false;
    }
}

在这里插入图片描述

三、二叉树的最大深度

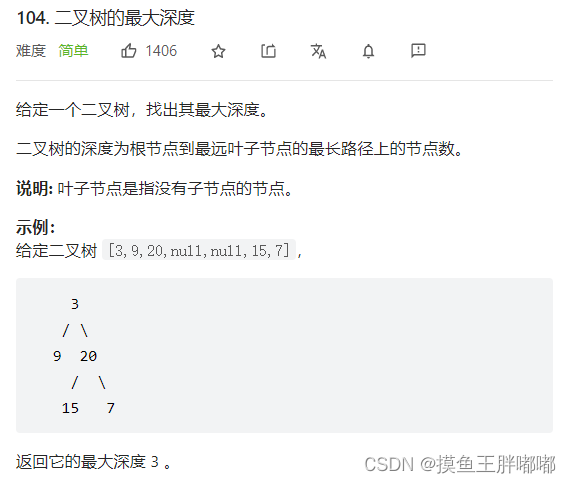
在这里插入图片描述

3.1 题解

方法：深度优先搜索

二叉树的最大深度无非就是左子树和右子树的最大深度+1，二叉树根节点为null的话，返回0。

3.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
    }
}

在这里插入图片描述

四、二叉树的前序遍历

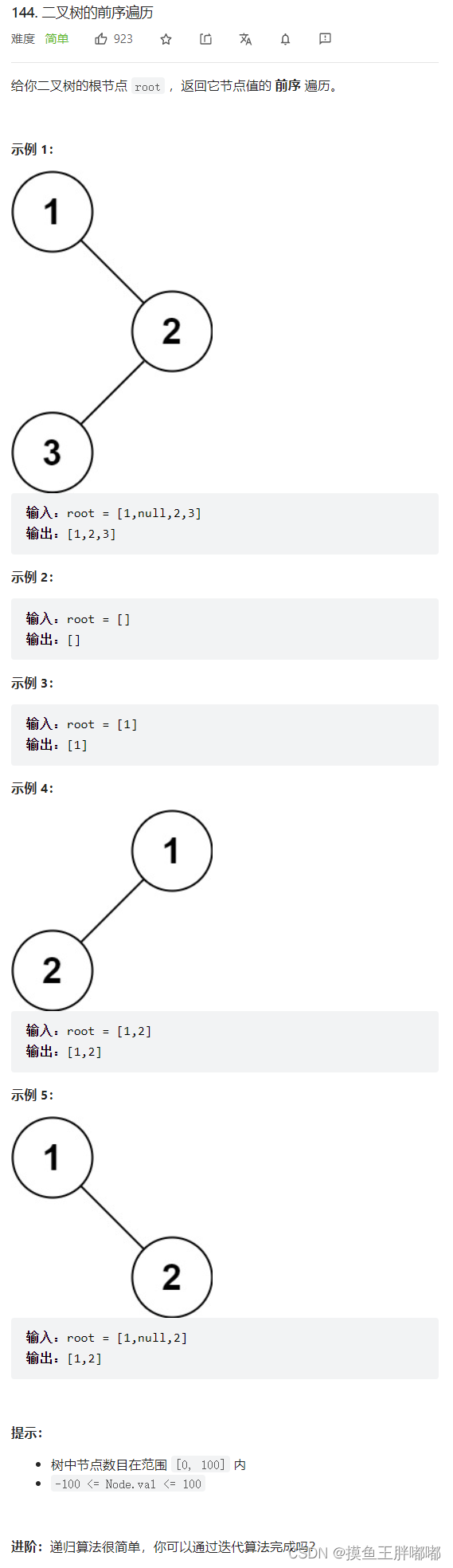
在这里插入图片描述

4.1 题解

方法：递归

每访问到一个节点如何给它存起来，那么我们定义一个顺序表来存储！

4.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> retlist = new ArrayList<>();
        if (root == null) {
            return retlist;
        }
        retlist.add(root.val);
        List<Integer> leftTree = preorderTraversal(root.left);
        retlist.addAll(leftTree);
        List<Integer> rightTree = preorderTraversal(root.right);
        retlist.addAll(rightTree);
        return retlist;
    }
    
}

在这里插入图片描述

五、二叉树的中序遍历

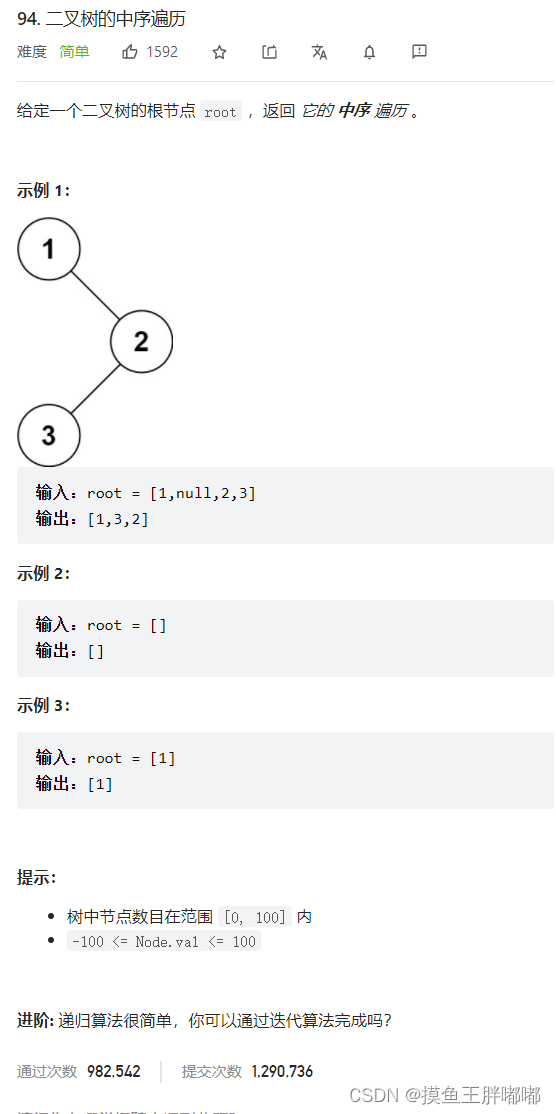
在这里插入图片描述

5.1 题解

方法：递归

同上题。

5.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> retlist = new ArrayList<>();
        if (root == null) {
            return retlist;
        }
       
        List<Integer> leftTree = inorderTraversal(root.left);
        retlist.addAll(leftTree);
        retlist.add(root.val);
        List<Integer> rightTree = inorderTraversal(root.right);
        retlist.addAll(rightTree);
        return retlist;
    }
}

在这里插入图片描述

六、二叉树的后序遍历

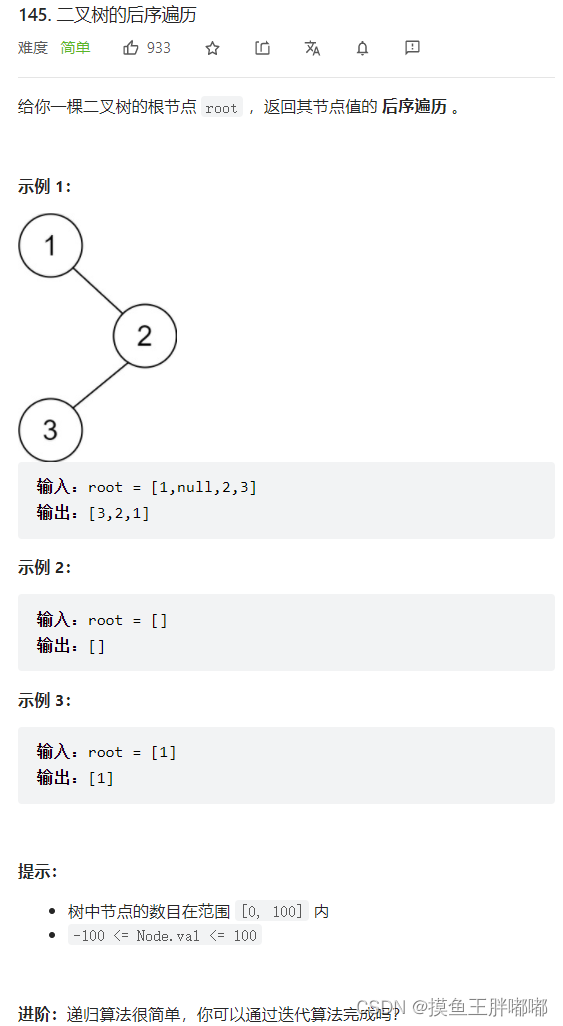
在这里插入图片描述

6.1 题解

方法：递归

同上题。

6.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> retlist = new ArrayList<>();
        if (root == null) {
            return retlist;
        }
        List<Integer> leftTree = postorderTraversal(root.left);
        retlist.addAll(leftTree);
       

        List<Integer> rightTree = postorderTraversal(root.right);
        retlist.addAll(rightTree);
         retlist.add(root.val);
        return retlist;
    }
}

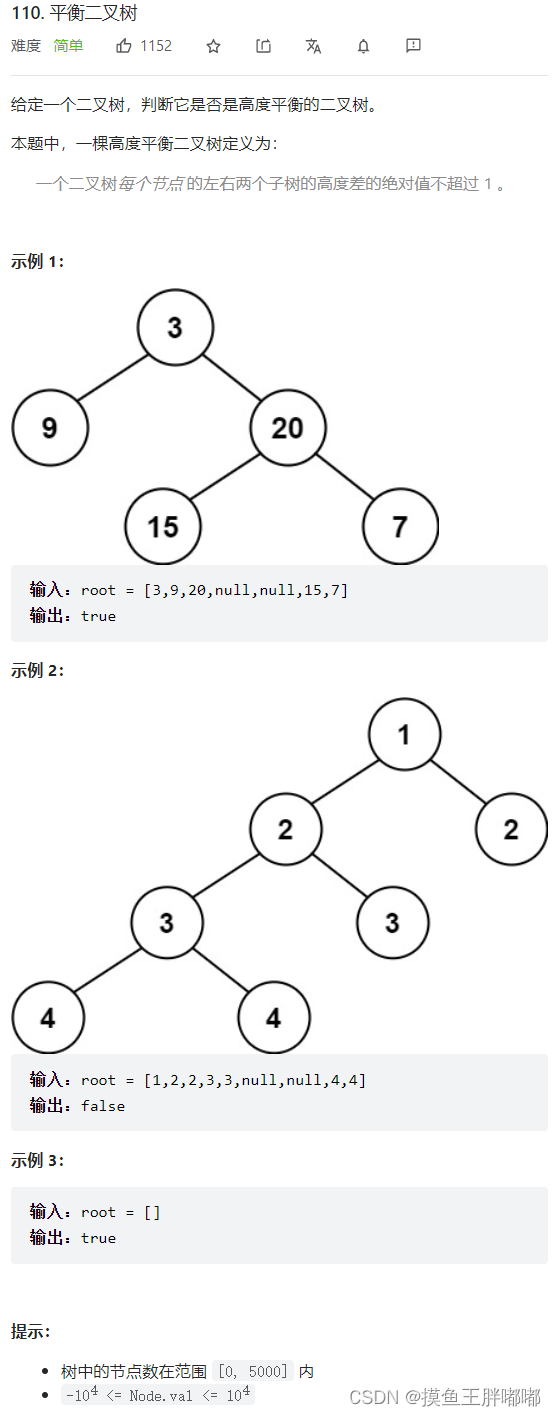
在这里插入图片描述

七、平衡二叉树

在这里插入图片描述

7.1 题解

方法一：自顶向下递归

具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，如果左右子树的高度差是否不超过 1，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。
在这里插入图片描述

方法二：自低向上递归

方法一由于是自顶向下递归，因此对于同一个节点，函数 height 会被重复调用，导致时间复杂度较高。如果使用自底向上的做法，则对于每个节点，函数 height 只会被调用一次。

自底向上递归的做法类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回 -1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。
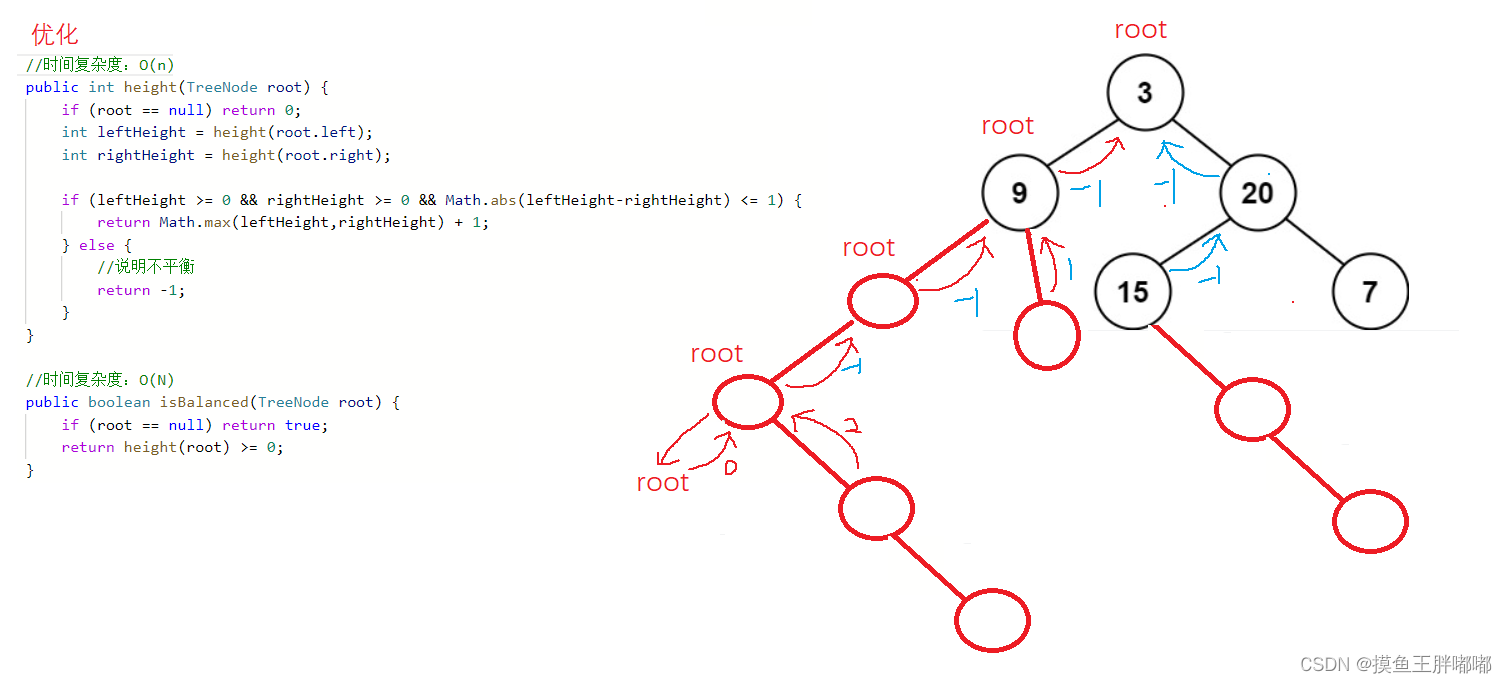
在这里插入图片描述

7.2 代码实现

方法一：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
/**
     * 求树的高度
     * @param root
     * @return
     */
    //时间复杂度：O(n)
    public int height(TreeNode root) {
        if (root == null) return 0;
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        return (leftHeight > rightHeight) ? (leftHeight+1) : (rightHeight+1);
    }
    /**
     * 平衡二叉树
     * @param root
     * @return
     */
    //时间复杂度：O(N^2)
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        int left = height(root.left);
        int right = height(root.right);

        return Math.abs(left-right) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

在这里插入图片描述

方法二：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    
    //时间复杂度：O(n)
    public int height(TreeNode root) {
        if (root == null) return 0;
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        
        if (leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <= 1) {
            return Math.max(leftHeight,rightHeight) + 1;
        } else {
            //说明不平衡
            return -1;
        }
    }

    //时间复杂度：O(N)
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        return height(root) >= 0;
    }
}

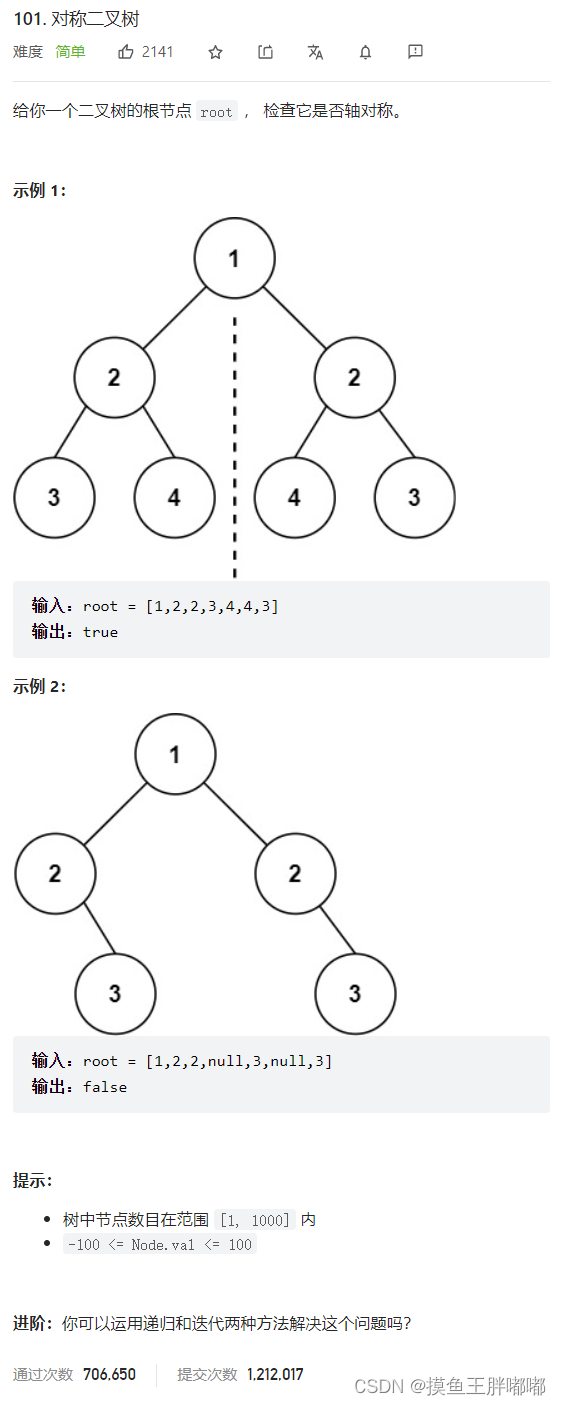
在这里插入图片描述

八、对称二叉树

在这里插入图片描述

8.1 题解

方法：递归

树根为空，返回true，左右子树都为null，返回true，判断左子树和右子树的值是否相同，否则直接返回false，递归判断左子树的左树和右子树的右树，左子树的右树和右子树的左树是否相同。
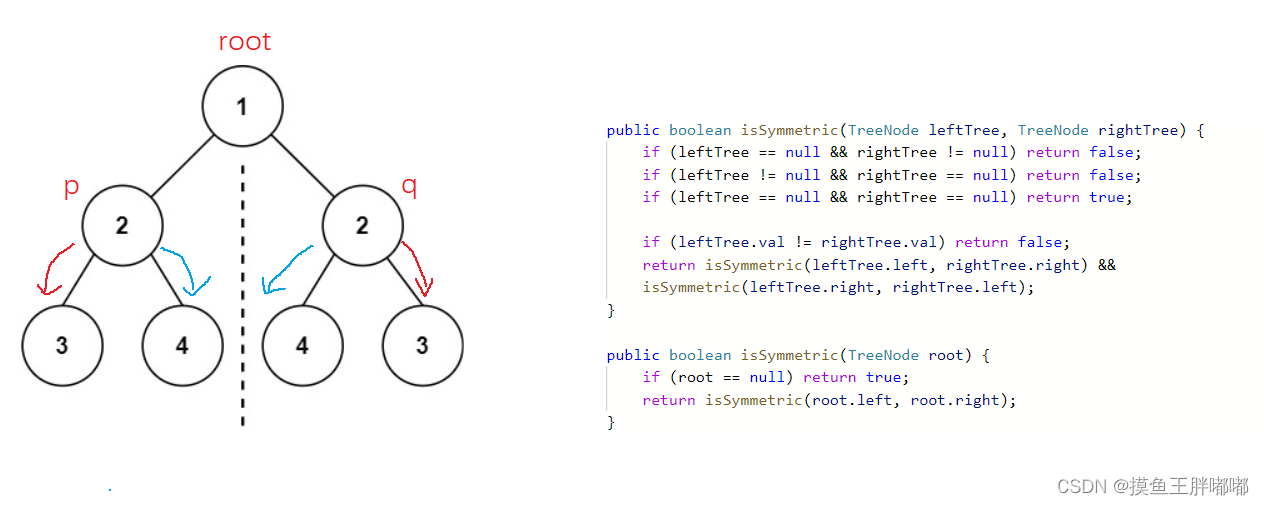
在这里插入图片描述

8.2 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    public boolean isSymmetric(TreeNode leftTree, TreeNode rightTree) {
        if (leftTree == null && rightTree != null) return false;
        if (leftTree != null && rightTree == null) return false;
        if (leftTree == null && rightTree == null) return true;

        if (leftTree.val != rightTree.val) return false;
        return isSymmetric(leftTree.left, rightTree.right) && 
        isSymmetric(leftTree.right, rightTree.left);
    }

    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        return isSymmetric(root.left, root.right);
    }
}

在这里插入图片描述

相关文章：

  • 江苏网站优化建站/赣州seo推广
  • 中小企业网站建设价格/百度搜索大数据
  • 做服装搭配的流行趋势网站/重庆seo公司排名
  • 网站开发android客户端/网站被百度收录
  • 网站成本费用/友情链接网站
  • 合肥网站建设套餐/成都网站seo费用
  • 【快速排序】
  • 大闸蟹提货系统asp版源码提供
  • 【简单dp】舔狗舔到最后一无所有
  • QML 应用程序
  • cicd的部署--gitlab
  • 基于JAVA地铁舆情管理系统计算机毕业设计源码+系统+lw文档+部署
  • 【leetcode24-----1比特与2比特字符】
  • Redis第二天
  • 【计算机毕业设计】Java ssm 高校运动会管理系统（开题+源码+论文）
  • Linux文件目录指令
  • 【Shading】Shadow Mapping 阴影映射
  • 数据结构与算法——线性表