数学基础从高一开始1、集合的概念

数学基础从高一开始1、集合的概念
目录
数学基础从高一开始1、集合的概念
一、课程引入
解析:方程编辑=2是否有解?
解析:所有到定点的距离等于定长的点组成何种图形?
结论:
二、课程讲解
问题1:
集合的特性:
问题2:
知识点小结1:
符号解析1:
问题3:
知识点小结2:
问题4:
练习:
练习1:
练习2:
练习3:
练习4:
符号解析2:
知识点小结3:
问题5:
问题6:
问题7:
三、例题讲解
例1、选择适当的方式表示下列集合:
四、总结
一、课程引入
1、方程
=2是否有解?
2、所有到定点的距离等于订场的点组成何种图形?
解析:方程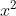 =2是否有解?
=2是否有解?
在有理数范围是没有解,在实数范围有2个根,
。
解析:所有到定点的距离等于定长的点组成何种图形?
在同一【平面内】组成:【圆】
在同一【空间】组成:【球面】
结论:
明确研究对象,明确研究范围是我们研究数学的基础问题。
二、课程讲解
问题1:
如何简洁、准确地描述数学对象及研究范围呢?我们看下面几个例子:
1、1~11之间的所有偶数;(蓝桥杯基础题)
2、衡水一中今年入学的全体高一学生;
3、地球上的四大洋;
4、不等式x-7<3的解集;
5、较小的数;
问题1的1、中,我们把1~11之间的每一个偶数即2/4/6/8/10作为研究对象,可以使用【i%2==0】的方式进行计算机计算,确定有数量范围。
问题1的2、中,衡水一中今年入学的每一个高一学生作为研究对象。肯定是有数量范围的。
一般地,我们把研究对象统称为【元素element】,把一些元素组成的总体叫做集合(set),简称集。无序,这里可以当做hashset,如果是treeset就是有序的。这里没有讨论list与map。
集合的特性:
1、集合具有确定性
2、集合具有互异性
3、集合具有无序性
问题2:
上面的问题1/3,问题1/4,问题1/5能组成集合吗?
【3、地球上的四大洋;】与【4、不等式x-7<3的解集;】是可以组成集合的,因为符合集合的确定性、互异性、无序性。但是【5、较小的数;】没有确定性,所以无法组成集合。
知识点小结1:
我们通常用大写拉丁字母A,B,C,……表示集合,用小写拉丁字母a,b,c,……表示集合中的元素。
如果a是集合A的元素,就说a属于(belong to)集合A,记作a∈A;如果a不是集合A的元素,就说a不属于(not belong to)集合A,记作a∉A。
符号解析1:
高中的第一个数学符号属于符号∈,对应的不属于符号∉。
问题3:
若用A表示前面问题(1)中“1~11之间的每一个偶数”组成的集合,3,4分组与集合A有何种关系呢?如何用数学语言表述呢?
易知4是A中的元素,3不是A中的元素,即:4∈A,3∉A。
知识点小结2:
全体非负整数组成的集合成为非负整数集(或自然数集),记作N;
全体正整数组成的集合成为正整数集,记作N*或
;
全体整数组成的集合称为整数集,记作Z;
全体有理数组成的集合称为有理数集,记作Q;
全体实数组成的集合称为实数集,记作R。
集合论的创立过程体现了数学发生发展的背景和客观需求,数学的发现和创造过程充满着数学家的想象力、创造力和不屈不挠、精益求精的精神,展现了人类理性思维的巨大力量。
问题4:
上面的例子中,我们用自然语言描述了一个集合,除此之外,还可以使用什么方式表示集合呢?
“方程
=2在实数范围内的根?”可以表示为{
,-
},
“1~11之间的所有偶数”组成的集合可以表示为{2,4,6,8,10},
“地球上的四大洋”组成的集合可以表示为{"太平洋","大西洋","印度洋","北冰洋"}。
练习:
练习1:
想这样把集合的所有元素一一列举出来,并用花括号括起来表示集合的方法叫做列举法。
列举法表示集合:
1、大于1且小于6的整数;
Set={2,3,4,5}
2、方程-9=0的所有实数根组成的集合;
Set={3,-3}
练习2:
0与{0}的数学含义相同吗?
不同,0表示数字0,{0}是列举法表示的集合,包含一个元素0.
练习3:
如何用数学语言表述0与{0}之间关系呢?
0与{0}是元素与集合的关系,元素0属于集合{0},记作0∈{0}.
练习4:
对于集合“所有到定点的距离等于订场的点组成何种图形?与不等式x-7<3的解集;”应该如何表示?
例如:不等式x-7<3的解集;
我们可以利用解集中元素的共同特征,即x是实数,且x<10,把解集表示为{x∈R|x<10}。
符号解析2:
|一个竖线,代表或,就是满足x∈R或x<10,这两个数值范围都是解集。
知识点小结3:
一般地,设A是一个集合,我们把集合A中所有具有共同特征P(x)的元素x所组成的集合表示为{x属于A|P(x)},这种表示集合的方式成为描述法。有时也用冒号或分号代替竖线,写成{x∈A:P(x)}或{x∈A;P(x)}。
问题5:
整数集Z可以分为奇数集和偶数集,我们如何用描述法表示奇数集?
可以确定任何数k*2+1都会是一个偶数,那么就可以表示为:x=2k+1,但x∈Z,k∈Z。
具体的表达集合的方式为:{x∈Z|x=2k+1,k∈Z}。
问题6:
用描述法描述偶数集?
表示方式:{x∈Z|x=2k,k∈Z}
问题7:
描述有理数集?
表示方式:Q={p/q|p∈Z,q∈N+且p与q互质}。
三、例题讲解
例1、选择适当的方式表示下列集合:
1、小于10的所有自然数组成的集合。
2、方程=x的所有实数根组成的集合。
小于10的自然数:A={0,1,2,3,4,5,6,7,8,9},描述法{x∈N|x<10},
代码描述:
x=0 for i in range(0,10): print(i)或
if x>0 and x<10 : print("集合A",x)方程
=x的所有实数根:B={0,1},这个求解也就知道了。
也可以用描述法:{x|
=x}。x∈R是明确的,R是所有实数的集合,叫实数集。省略了。
练习8:
解,设x∈A,则x是一个实数,且-2x-3=0。因此,用描述法表示为:A={x|
-2x-3=0},
方程 -2x-3=0有两个实数根3与-1,用列举法表示:A={3,-1}。
四、总结
由于有理数集中所有元素均为有理数,因此可得:
整数集、分数集、小数集、自然数集,都是有理数集的一个子集即:
有理数包含整数、分数、小数、自然数等(不考虑重复列举关系)。
有理数集是实数集的一个子集,也是复数集的一个子集即:
有理数是实数(或复数)的一部分。
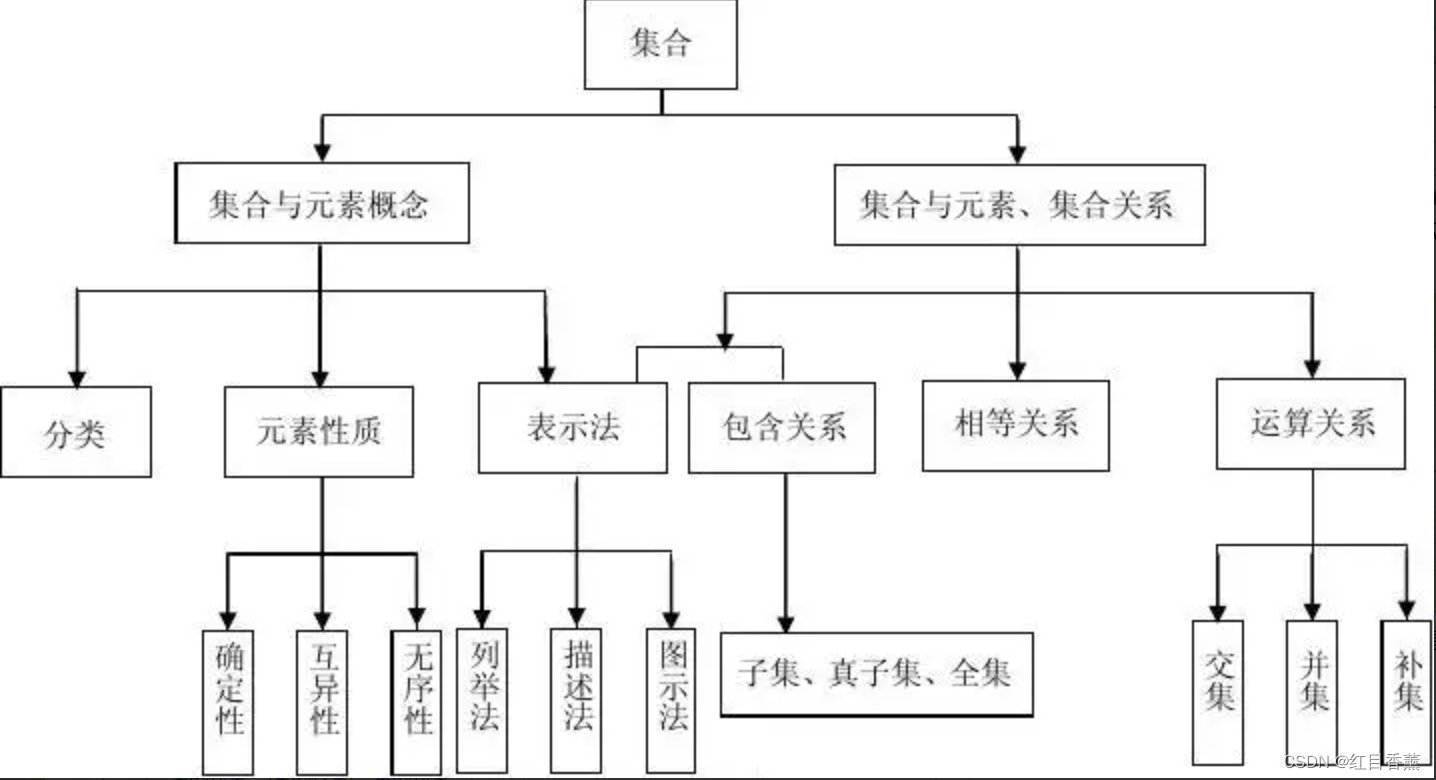
注意符号都表表什么,如何使用。
这里是比较抽象的,需要大脑进行抽象思维模式的思考。
