当前位置：首页 > news >正文

17-JavaSE基础巩固练习：Math类API两道数学算法水题

news 来源：原创 2024/12/25 23:19:21

两道算法水题（一）

一、判断质数

判断一个数是否为一个质数。

1、以前的写法

package com.app.demo26_math_api;

public class Test1 {
    public static void main(String[] args) {
        /*
            判断n(任意整数)是否为一个质数：
                以前的写法:
                    是用n对2~n之间的每一个数进行求余，
                    如果为0就不是质数，否则就为质数。
         */
        System.out.println(isPrime(997));
    }

    /**
     * 判断n是否为一个质数
     * @param n 任意整数
     * @return  是则返回true，否则返回false
     */
    private static boolean isPrime(int n) {
        int count = 0;
        for (int i = 2; i < n; i++) {
            count++;    // 每循环1次，计数
            if (n % i == 0) {
                return false;
            }
        }
        System.out.println("循环了：" + count + "次");
        return true;
    }
}

循环了：995次
true

Process finished with exit code 0

可以看到，以前的写法，需要循环2~n之间的每一个数，效率非常的低！

2、优化写法

（1）思考

从下面的数之中，可以看到什么规律吗？
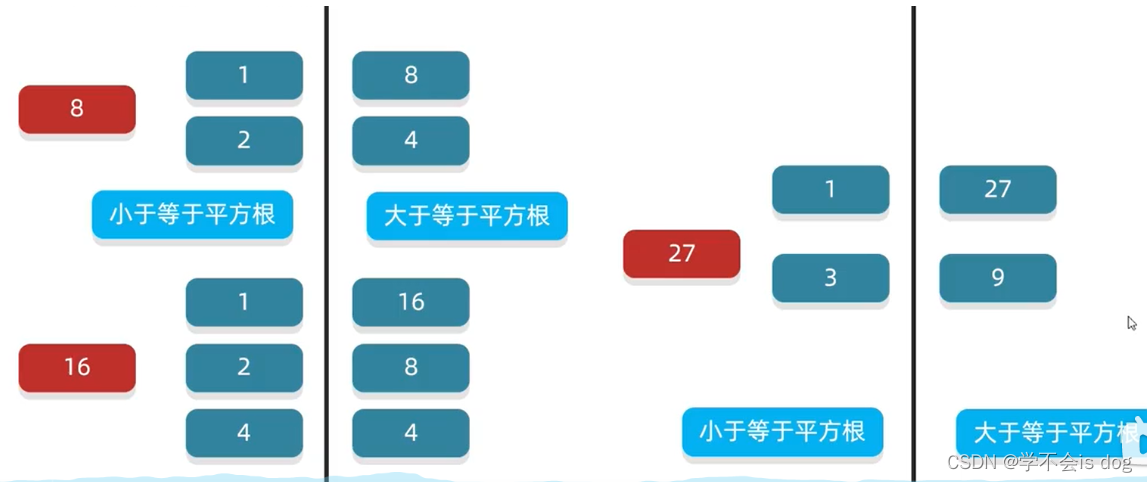
拿16举个例子：
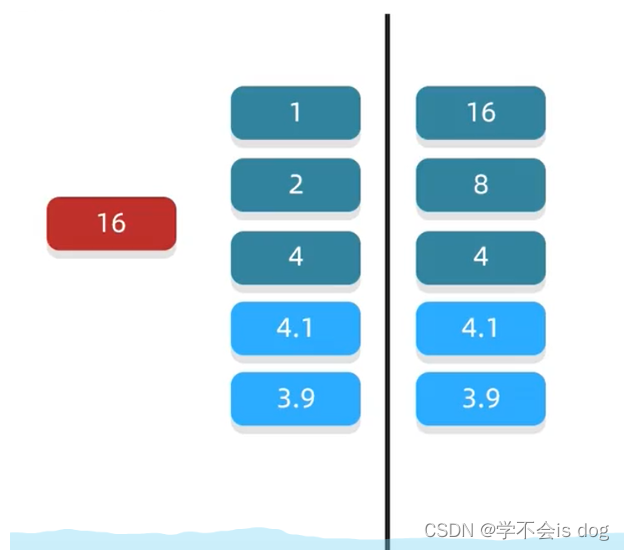
- 16的平方根是4，那么4.1和4.1相乘是不是就不可能等于16？
- 那么3.9和3.9相乘是不是就不可能等于16？
- 回答：是的，因此总结出规律，一个整数的任意一对因子中，左边都是小于等于平方根的，右边都是大于等于平方根的。

（2）结论

一个整数的任意一对因子中，左边都是小于等于平方根的，右边都是大于等于平方根的。
由于一个任意整数的因子都是成双成对出现的，因此我们只需要判断平方根左边的数就可以了！
就不需要循环得到2到任意整数之间的每个数来判断了！
注意：必须包含平方根本身，因为因子是一对一对出现的，而平方根就是中间点！

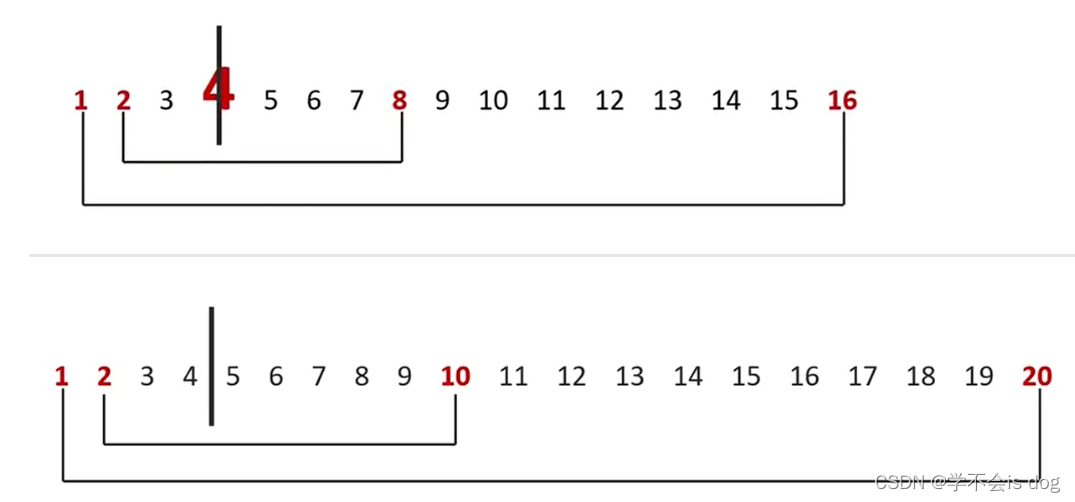
在这里插入图片描述

（3）实现

package com.app.demo26_math_api;

public class Test1Plus {
    public static void main(String[] args) {
        /*
            判断n(任意正整数)是否为一个质数：
                优化写法:
                    是用n对2~n的平方根之间的每一个数（包含平方根本身）进行求余，
                    如果为0就不是质数，否则就为质数。
         */
        System.out.println("997是质数：" + isPrime(997));
    }

    /**
     * 判断n是否为一个质数
     *
     * @param n 任意正整数
     * @return 是则返回true，否则返回false
     */
    private static boolean isPrime(int n) {
        int count = 0;
        // Math类的sqrt(): 返回值的正确舍入正平方根
        for (int i = 2; i <= Math.sqrt(n); i++) {
            count++;    // 每循环1次，计数
            if (n % i == 0) {
                return false;
            }
        }
        System.out.println("循环了：" + count + "次");
        return true;
    }
}

循环了：30次
997是质数：true

Process finished with exit code 0

可以看到，只循环了30次，大大提高了效率！

两道算法水题（二）

1、思考

自幂数，一个n位自然数等于自身各个数位上数字的n次幂之和。
举例1：三位数
- 1^3 + 5^3 + 3^3 = 153
举例2：四位数
- 1^4 + 6^4 + 3^4 + 4^4=1634

如果自幂数是一位数，也叫做：独身数
三位自幂数：水仙花数
四位自幂数：四叶玫瑰数
五位自幂数：五角星数
六位自幂数：六合数
七位自幂数：北斗七星数
八位自幂数：八仙数
九位自幂数：九九重阳数
十位自幂数：十全十美数

2、需求

1、统计一共有多少个水仙花数。
2、证明没有两位的自幂数。
3、分别统计有多少个四叶玫瑰数和五角星数。(答案是3个)

3、实现

（1）以前的写法

package com.app.demo26_math_api;

public class Test2 {
    public static void main(String[] args) {
        /*
            1、统计一共有多少个水仙花数。
            2、证明没有两位的自幂数。
            3、分别统计有多少个四叶玫瑰数和五角星数。(答案都是3个)
         */
        narcissisticNumber();   // 水仙花数
        System.out.println("两位的自幂数存在吗：" + noTwoSelfPowerNumber() + "\n"); // 证明两位的自幂数是不存在的
        fourLeafNumber();       // 四叶玫瑰数
        fivePointedNumber();    // 五角星数
    }

    /**
     * 统计五角星数
     */
    private static void fivePointedNumber() {
        int count = 0;
        for (int i = 10000; i < 99999; i++) {
            // 依次得到当前数的个位、十位、百位、千位、万位数
            int ge = i % 10;
            int shi = i / 10 % 10;
            int bai = i / 100 % 10;
            int qian = i / 1000 % 10;
            int wan = i / 10000 % 10;

            // 统计每一位的五次方之和
            int sum = ge*ge*ge*ge*ge + shi*shi*shi*shi*shi + bai*bai*bai*bai*bai + qian*qian*qian*qian*qian + wan*wan*wan*wan*wan;
            // 判断当前数的五次方之和 是否与本身 相等
            if (sum == i) {
                // 是，则说明当前数是四叶玫瑰数，统计个数并输出
                count++;
                System.out.println(i);
            }
        }
        System.out.println("五角星数有" + count + "个。\n");
    }

    /**
     * 统计四叶玫瑰数
     */
    private static void fourLeafNumber() {
        int count = 0;
        for (int i = 1000; i < 9999; i++) {
            // 依次得到当前数的个位、十位、百位、千位数
            int ge = i % 10;
            int shi = i / 10 % 10;
            int bai = i / 100 % 10;
            int qian = i / 1000 % 10;

            // 统计每一位的四次方之和
            int sum = ge*ge*ge*ge + shi*shi*shi*shi + bai*bai*bai*bai + qian*qian*qian*qian;
            // 判断当前数的四次方之和 是否与本身 相等
            if (sum == i) {
                // 是，则说明当前数是四叶玫瑰数，统计个数并输出
                count++;
                System.out.println(i);
            }
        }
        System.out.println("四叶玫瑰数有" + count + "个。\n");
    }

    /**
     * 判断是否有两位的自幂数
     * @return 有则返回true，否则返回false
     */
    private static boolean noTwoSelfPowerNumber() {
        for (int i = 10; i <= 99; i++) {
            // 依次得到该数的个位、十位数
            int ge = i % 10;
            int shi = i / 10 % 10;

            // 每一位的二次方之和
            int sum = ge*ge + shi*shi;
            // 判断每一位的二次方之和 是否等于当前数
            if (sum == i) {
                // 是，则说明两位的自幂数存在，输出并返回true
                System.out.println(i);
                return true;
            }
        }
        // 循环结束，说明两位的自幂数不存在，返回false
        return false;
    }

    /**
     * 统计水仙花数的个数
     */
    private static void narcissisticNumber() {
        // 定义计数器
        int count = 0;

        for (int i = 100; i <= 999; i++) {
            // 依次得到该数的个位、十位、百位数
            int ge = i % 10;
            int shi = i / 10 % 10;
            int bai = i / 100 % 10;
            // 以前的写法：
            // 每一位的三次方之和 跟本身 进行比较
            int sum = ge*ge*ge + shi*shi*shi + bai*bai*bai;
            // 判断是否相等
            if (sum == i) {
                // 是，则说明该数是水仙花数，统计个数并且输出
                count++;
                System.out.println(i);
            }
        }

        System.out.println("水仙花数有" + count + "个。\n");
    }
}

153
370
371
407
水仙花数有4个。

两位的自幂数存在吗：false

1634
8208
9474
四叶玫瑰数有3个。

54748
92727
93084
五角星数有3个。


Process finished with exit code 0

可以看到，虽然实现出来了，但是代码还是不太优雅！
比如:
```
ge*ge*ge*ge*ge + shi*shi...
```
- 这样的代码非常冗长！

（2）优化写法

package com.app.demo26_math_api;

public class Test2Plus {
    public static void main(String[] args) {
        /*
            1、统计一共有多少个水仙花数。
            2、证明没有两位的自幂数。
            3、分别统计有多少个四叶玫瑰数和五角星数。(答案都是3个)
         */
        narcissisticNumber();   // 水仙花数
        System.out.println("两位的自幂数存在吗：" + noTwoSelfPowerNumber() + "\n"); // 证明两位的自幂数是不存在的
        fourLeafNumber();       // 四叶玫瑰数
        fivePointedNumber();    // 五角星数
    }

    /**
     * 统计五角星数
     */
    private static void fivePointedNumber() {
        int count = 0;
        for (int i = 10000; i < 99999; i++) {
            // 依次得到当前数的个位、十位、百位、千位、万位数
            int ge = i % 10;
            int shi = i / 10 % 10;
            int bai = i / 100 % 10;
            int qian = i / 1000 % 10;
            int wan = i / 10000 % 10;

            // 统计每一位的五次方之和
            /*
                Math类的pow(double a, double b):
                    API作用：返回a的值的b次幂
                    double a(参数一)：值本身
                    double b(参数二)：多少次幂
             */
            double sum = Math.pow(ge, 5) + Math.pow(shi, 5) + Math.pow(bai, 5) + Math.pow(qian, 5) + Math.pow(wan, 5);
            // 判断当前数的五次方之和 是否与本身 相等
            if (sum == i) {
                // 是，则说明当前数是四叶玫瑰数，统计个数并输出
                count++;
                System.out.println(i);
            }
        }
        System.out.println("五角星数有" + count + "个。\n");
    }

    /**
     * 统计四叶玫瑰数
     */
    private static void fourLeafNumber() {
        int count = 0;
        for (int i = 1000; i < 9999; i++) {
            // 依次得到当前数的个位、十位、百位、千位数
            int ge = i % 10;
            int shi = i / 10 % 10;
            int bai = i / 100 % 10;
            int qian = i / 1000 % 10;

            // 统计每一位的四次方之和
            /*
                Math类的pow(double a, double b):
                    API作用：返回a的值的b次幂
                    double a(参数一)：值本身
                    double b(参数二)：多少次幂
             */
            double sum = Math.pow(ge, 4) + Math.pow(shi, 4) + Math.pow(bai, 4) + Math.pow(qian, 4);
            // 判断当前数的四次方之和 是否与本身 相等
            if (sum == i) {
                // 是，则说明当前数是四叶玫瑰数，统计个数并输出
                count++;
                System.out.println(i);
            }
        }
        System.out.println("四叶玫瑰数有" + count + "个。\n");
    }

    /**
     * 判断是否有两位的自幂数
     * @return 有则返回true，否则返回false
     */
    private static boolean noTwoSelfPowerNumber() {
        for (int i = 10; i <= 99; i++) {
            // 依次得到该数的个位、十位数
            int ge = i % 10;
            int shi = i / 10 % 10;

            // 每一位的二次方之和
            /*
                Math类的pow(double a, double b):
                    API作用：返回a的值的b次幂
                    double a(参数一)：值本身
                    double b(参数二)：多少次幂
             */
            double sum = Math.pow(ge, 2) + Math.pow(shi, 2);
            // 判断每一位的二次方之和 是否等于当前数
            if (sum == i) {
                // 是，则说明两位的自幂数存在，输出并返回true
                System.out.println(i);
                return true;
            }
        }
        // 循环结束，说明两位的自幂数不存在，返回false
        return false;
    }

    /**
     * 统计水仙花数的个数
     */
    private static void narcissisticNumber() {
        // 定义计数器
        int count = 0;

        for (int i = 100; i <= 999; i++) {
            // 依次得到该数的个位、十位、百位数
            int ge = i % 10;
            int shi = i / 10 % 10;
            int bai = i / 100 % 10;
            // 优化写法：
            // 每一位的三次方之和 跟本身 进行比较
            /*
                Math类的pow(double a, double b):
                    API作用：返回a的值的b次幂
                    double a(参数一)：值本身
                    double b(参数二)：多少次幂
             */
            double sum = Math.pow(ge, 3) + Math.pow(shi, 3) + Math.pow(bai, 3);
            // 判断是否相等
            if (sum == i) {
                // 是，则说明该数是水仙花数，统计个数并且输出
                count++;
                System.out.println(i);
            }
        }

        System.out.println("水仙花数有" + count + "个。\n");
    }
}

153
370
371
407
水仙花数有4个。

两位的自幂数存在吗：false

1634
8208
9474
四叶玫瑰数有3个。

54748
92727
93084
五角星数有3个。


Process finished with exit code 0

代码优化了，实现结果也一样！

58同城泉州网站建设/北京搜索优化排名公司

wordpress 4.7.2 更新/深圳seo专家

长春火车站是北站吗/设计模板网站

购物网站建设合同/天津seo结算

注册一个劳务公司需要多少钱/沈阳关键词seo

创意合肥网站建设/上海广告公司排名

[附源码]JAVA毕业设计课程答疑系统（系统+LW）

7 8051 C51 使用_getkey对scanf输入重定向，实现标准输入输出，getchar

逻辑回归模型和Python代码实现

Web 性能测试

关于小程序session_key漏洞问题的解决2022-12-01

基于MSER的高速公路交通标志提取matlab仿真

ARM 重定位引入和链接脚本

文本编辑器vi--常用命令查阅版（记得收藏）

HIN应用调研总结

基于UDP的服务器端和客户端

极简的Http请求client推荐-OkHttp

Nginx配置实例-反向代理

两道算法水题（一）

一、判断质数

1、以前的写法

2、优化写法

（1）思考

（2）结论

（3）实现

两道算法水题（二）

1、思考

2、需求

3、实现

（1）以前的写法

（2）优化写法

相关文章：