【AI】Best-first search (or Greedy Search) 最佳优先搜索(或贪婪搜索)
本博客讨论什么是最佳优先搜索,或称贪婪搜索。
本博客将借助多个示例去引入贪婪搜索的相关知识与概念。以助于理解掌握。
贪婪搜索算法概述
贪婪搜索算法的思想,是通过对比相邻点中哪个与目标点的距离最短来确定。
示例如下
e
.
g
.
e.g.
e.g. A城市 有两个相邻城市,B与C;B城市 有两个相邻城市,A与E;C城市 也有两个相邻城市,A与E。现在我们想从 A城市 到 E城市,但是无奈没有路,需要借道 B城市 或者 C城市,那么请问根据贪婪算法我们应该如何做出选择?
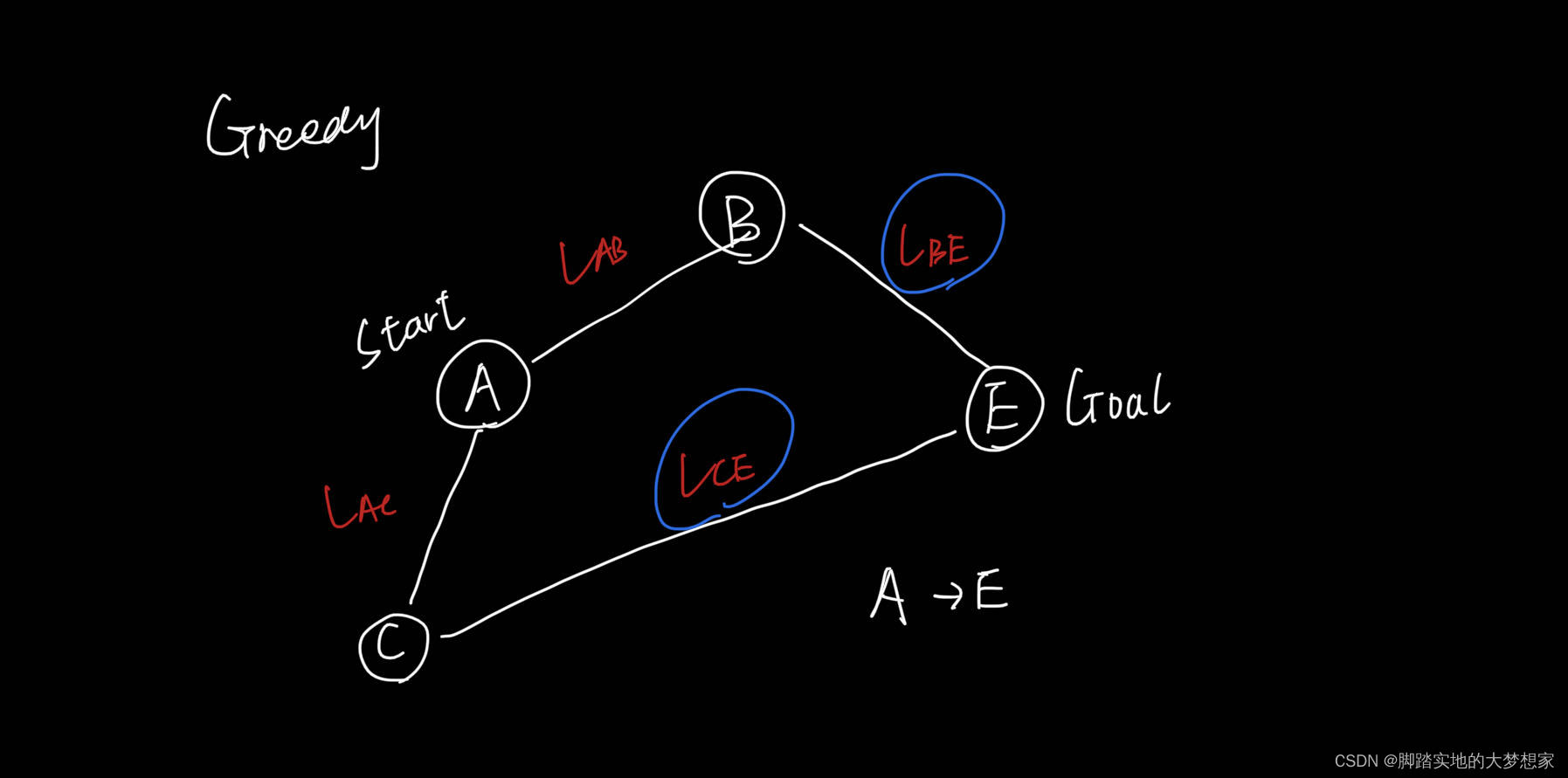
解答: 根据贪婪算法,我们计算 B城市 与 E城市 的距离 l B E l_{BE} lBE 以及 C城市 与 E城市 的距离 l C E l_{CE} lCE,计算结果为 l B E < l C E l_{BE}<l_{CE} lBE<lCE,所以我们选择从 A城市 途径 B城市 最终抵达 E城市。
现在我们来解决一个更为复杂的示例:
贪婪算法求“最短”路线
示例如下
e
.
g
.
e.g.
e.g. 用贪婪搜索尝试寻找 城市Arad 到 城市Bucharest 的“最短”路线。(图中已圈出)
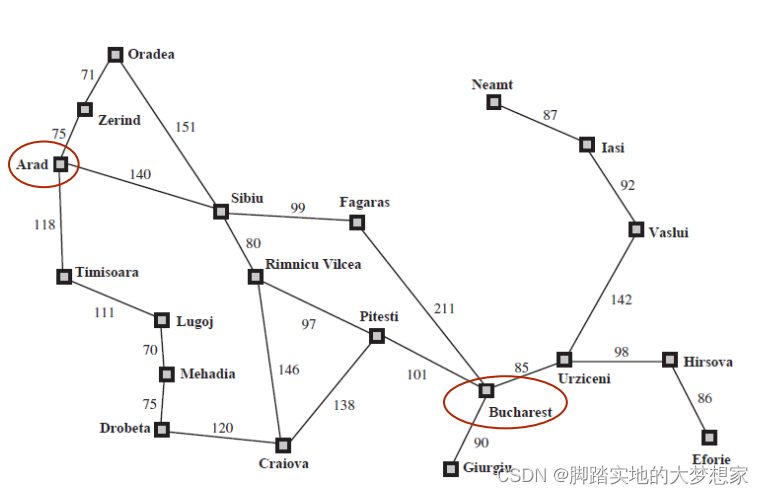
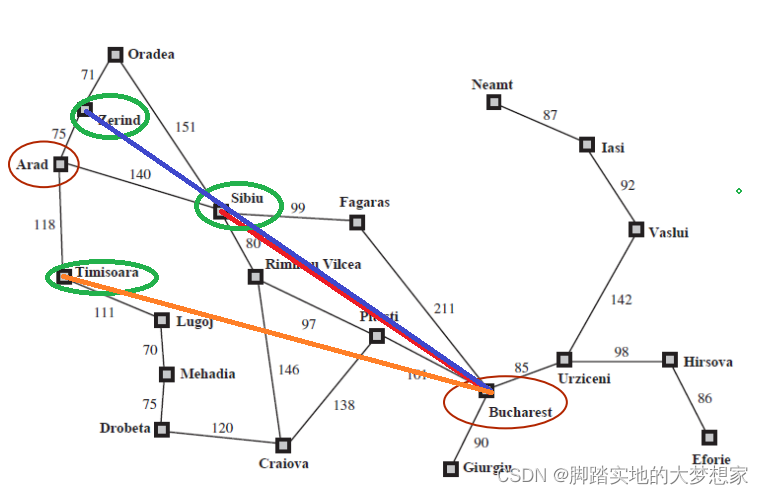
首先,起点 城市Arad 有三个相邻的城市 城市Zerind,城市Sibiu,城市Timisoara。根据贪婪算法,我们对这三个城市计算其与终点 城市Bucharest 的直线距离:
其实在这里会引出一个问题,那就是计算距离的时候用曼哈顿距离法还是用欧几里得距离法。在本道题中我们先默认使用欧几里得距离法,即“两点之间线段最短”的长度。本题末尾会讨论距离问题。
| 城市 | Distance |
|---|---|
| Zerind | 374 |
| Sibiu | 253 |
| Timisoara | 329 |
其实很明显,在与起点 城市Arad 相连的三个城市中,城市Sibiu 明显距离终点更近,所以我们选择 城市Sibiu 作为途径点。
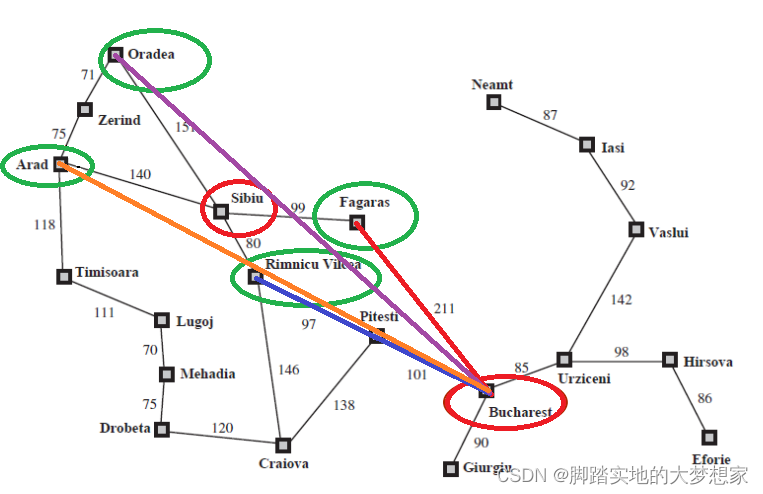
第二步,当我们抵达了 城市Sibiu 之后,需要考虑的问题是选择哪个城市作为下一个途径点呢?与 城市Sibiu 邻接的城市有 城市Oradea,城市Arad,城市Fagaras,城市Rimnicu Vilcea,我们对这四个城市计算其与终点 城市Bucharest 的直线距离:
| 城市 | Distance |
|---|---|
| Oradea | 380 |
| Arad | 366 |
| Fagaras | 176 |
| Rimnicu Vilcea | 193 |
明显,Fagaras “力排众议”,距离终点 城市Bucharest 最近,成为第二个途径点。
第三步,当我们抵达Fagaras后,开始选择下一个途径点。因为与Fagaras有两个邻接点,Sibiu 与 终点Bucharest,此时已不用多想,直接Bucharest。我们抵达了终点!
所以按照贪婪搜索算法,我们从初始点Arad到终点Bucharest的路线为:
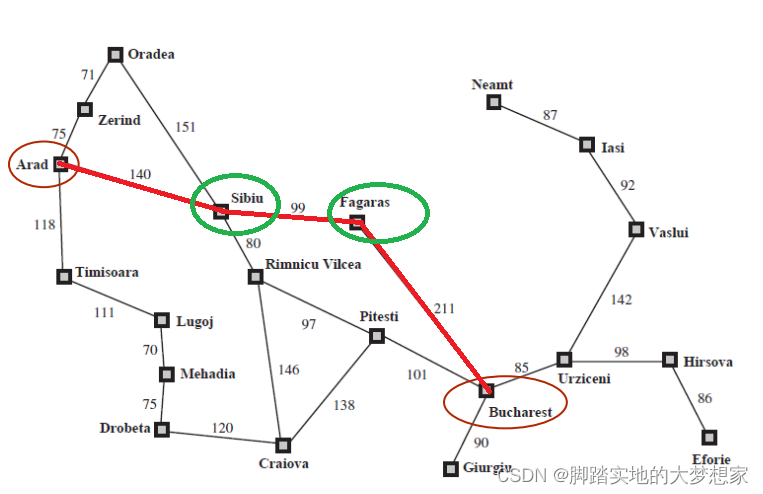
但是其实这个路线真的是最短路径吗?其实还真不是。所以我们通过贪婪搜索算法求得的路线,不一定为最短路径。
QA 在上体中可能遇到的问题
Q1:为什么Fagaras与Bucharest的距离是176不是标注的211?
A1:因为标注的距离并非直线距离,而是通过 城市Fagaras 抵达 城市Bucharest 的实际距离。往往一个城市到另一个城市之间是无法直接直线抵达的,本题目中标注的直线只是为了简化问题,方便读者理解。
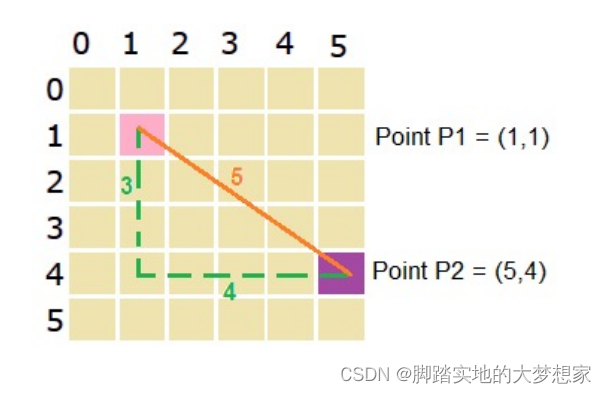
Q2:曼哈顿距离与欧几里得距离
A2:曼哈顿距离,指的是两点之间的距离要将x与y向量之间的距离分别求得 ( x 1 − x 2 ) + ( y 1 − y 2 ) (x_1-x_2)+(y_1-y_2) (x1−x2)+(y1−y2);而欧几里得,欧氏距离,通过两点之间的连线,即 ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt {(x_1-x_2)^2+(y_1-y_2)^2} (x1−x2)2+(y1−y2)2 求得。
M
a
n
h
a
t
t
a
n
D
i
s
t
a
n
c
e
=
∣
5
−
1
∣
+
∣
4
−
1
∣
=
7
Manhattan Distance = |5-1|+|4-1|=7
ManhattanDistance=∣5−1∣+∣4−1∣=7
E u c l i d e a n D i s t a n c e = ( 5 − 1 ) 2 + ( 4 − 1 ) 2 = 5 Euclidean Distance = \sqrt {(5-1)^2+(4-1)^2}=5 EuclideanDistance=(5−1)2+(4−1)2=5
Manhattan Distance 曼哈顿距离,主要应用场景为城市交通。在大多数城市,两个点之间的距离很难做到直线抵达。
d
(
x
i
,
x
j
)
=
∣
x
i
1
,
x
j
1
∣
+
∣
x
i
p
,
x
j
p
∣
+
.
.
.
+
∣
x
i
p
,
x
j
p
∣
d(x_i, x_j)=|x_{i1}, x_{j1}|+|x_{ip}, x_{jp}|+...+|x_{ip}, x_{jp}|
d(xi,xj)=∣xi1,xj1∣+∣xip,xjp∣+...+∣xip,xjp∣
Euclidean Distance 欧几里得距离,主要应用场景为数学。
d
(
x
i
,
x
j
)
=
∣
x
i
1
,
x
j
1
∣
2
+
∣
x
i
p
,
x
j
p
∣
2
+
.
.
.
+
∣
x
i
p
,
x
j
p
∣
2
d(x_i,x_j)=\sqrt {|x_{i1}, x_{j1}|^2+|x_{ip}, x_{jp}|^2+...+|x_{ip}, x_{jp}|^2}
d(xi,xj)=∣xi1,xj1∣2+∣xip,xjp∣2+...+∣xip,xjp∣2
在本题中,我们选择欧几里得距离作为我们的启发值。即我们用直线做的启发值。其释义是我们选择通过两城市之间的直线距离作为其之间的距离。
有关贪婪算法介绍到这里,是否存在问题,可留言~
