LeetCode每日一题系列

题目：902. 最大为 N 的数字组合
难度：困难

题目

给定一个按 非递减顺序 排列的数字数组 digits 。你可以用任意次数 digits[i] 来写的数字。例如，如果 digits = [‘1’,‘3’,‘5’]，我们可以写数字，如 ‘13’, ‘551’, 和 ‘1351315’。

返回 可以生成的小于或等于给定整数 n 的正整数的个数 。

示例

示例 1：

输入：digits = [“1”,“3”,“5”,“7”], n = 100
输出：20
解释： 可写出的 20 个数字是： 1, 3,5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.

示例 2：

输入：digits = [“1”,“4”,“9”], n = 1000000000
输出：29523
解释： 我们可以写 3 个一位数字，9个两位数字，27 个三位数字， 81 个四位数字，243 个五位数字，729 个六位数字， 2187 个七位数字，6561 个八位数字和19683 个九位数字。 总共，可以使用D中的数字写出 29523 个整数。

示例 3:

输入：digits = [“7”], n = 8
输出：1

提示：

1 <= digits.length <= 9
digits[i].length == 1
digits[i] 是从 ‘1’ 到 ‘9’ 的数
digits 中的所有值都 不同
digits 按 非递减顺序 排列
1 <= n <= 109

思路

数位dp：

1. 定义状态:我们用 dp[i][0]表示由 digits构成且小于n 的前 i 位的数字的个数，dp[i][1] 表示由 digits构成且等于 n 的前 i 位的数字的个数，可知 dp[i][1] 的取值只能为0 和 1。

2. n表示给定数字最大值，d表示digits中的数字，n的前i位组成的数字为n[i]，这里会遇到几种情况：
   1、当i>1时，任意digits中的d都小于等于s[:i]，这一情况下满足条件的数量为len(digits)
   2、当d<n[i-1]，我们任意再向后面加一位都满足条件，这一情况满足条件的数量为dp[i-1][0] * len(digits)
   3、当d=n[i-1]，我必须向后加一个小于n[i]的才满足条件，这一情况满足条件的数量为dp[i-1][0]*digits中小于n[i]的值

3. 我们初始将dp[0][1]设为1，遍历到后面如果发现digits中不含有某个n[i]，再将dp[i][1]设置为1

4. 设 C[i]表示数组 digits 中小于 n 的第 i 位数字的元素个数，综上所述，dp的状态转移方程为：
   

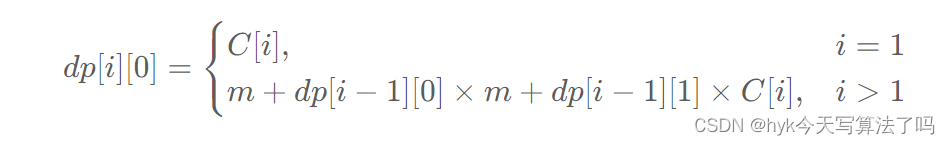
题解

class Solution:
    def atMostNGivenDigitSet(self, digits: List[str], n: int) -> int:
        m = len(digits)
        s = str(n)
        k = len(s)
        dp = [[0, 0] for _ in range(k + 1)]
        # 设置初始状态
        dp[0][1] = 1
        # 遍历n
        for i in range(1, k + 1):
        	# 遍历digits
            for d in digits:
            	# digits中存在n[i]
                if d == s[i - 1]:
                    dp[i][1] = dp[i - 1][1]
                # d小于n[i-1]，累加上dp[i-1][1]，属于当d=n[i-1]，我必须向后加一个小于n[i]的才满足条件的情况
                elif d < s[i - 1]:
                    dp[i][0] += dp[i - 1][1]
                else:
                    break
            # 当i>1，累加上所有情况即可
            if i > 1:
                dp[i][0] += m + dp[i - 1][0] * m
        # 返回最后一位dp[k][0]和dp[k][1]的和即可
        return sum(dp[k])