一、问题描述

[洛谷]P2234 [HNOI2002]营业额统计

题目描述

Tiger 最近被公司升任为营业部经理，他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。

Tiger 拿出了公司的账本，账本上记录了公司成立以来每天的营业额。分析营业情况是一项相当复杂的工作。由于节假日，大减价或者是其他情况的时候，营业额会出现一定的波动，当然一定的波动是能够接受的，但是在某些时候营业额突变得很高或是很低，这就证明公司此时的经营状况出现了问题。经济管理学上定义了一种最小波动值来衡量这种情况：当最小波动值越大时，就说明营业情况越不稳定。

而分析整个公司的从成立到现在营业情况是否稳定，只需要把每一天的最小波动值加起来就可以了。你的任务就是编写一个程序帮助 Tiger 来计算这一个值。

我们定义，一天的最小波动值 = min ⁡ { ∣ 该天以前某一天的营业额 − 该天营业额 ∣ } \min\{|\text{该天以前某一天的营业额}-\text{该天营业额}|\} min{∣该天以前某一天的营业额−该天营业额∣}。

特别地，第一天的最小波动值为第一天的营业额。

输入格式

第一行为正整数 $n$（$n\le 32767$） ，表示该公司从成立一直到现在的天数，接下来的 $n$ 行每行有一个整数 $a_i$（$|a_i|\le 10^6$) ，表示第 $i$ 天公司的营业额，可能存在负数。

输出格式

输出一个正整数，即每一天最小波动值的和，保证结果小于 $2^{31}$。

样例 #1

样例输入 #1

6
5
1
2
5
4
6

样例输出 #1

12

提示

结果说明：$5+|1-5|+|2-1|+|5-5|+|4-5|+|6-5|=5+4+1+0+1+1=12$

二、问题分析

1、算法标签

这道题考察的是容器$set$的使用。

2、思路分析

这道题的核心就是一件事情：给你一个数字$x$，而我们要找到数轴上距离$x$的最小值。而此时，我们就联想到了$set$容器中的一个函数:$lower$_$bound()$

我们传入一个参数$x$，这个函数的作用就是找到第一个不小于这个数的元素所在的位置，并返回这个位置的迭代器。如果不存在这个数的话，那么这个函数返回的就是最后一个元素的后一个位置的迭代器。

那么此时我们就分为三种情况：

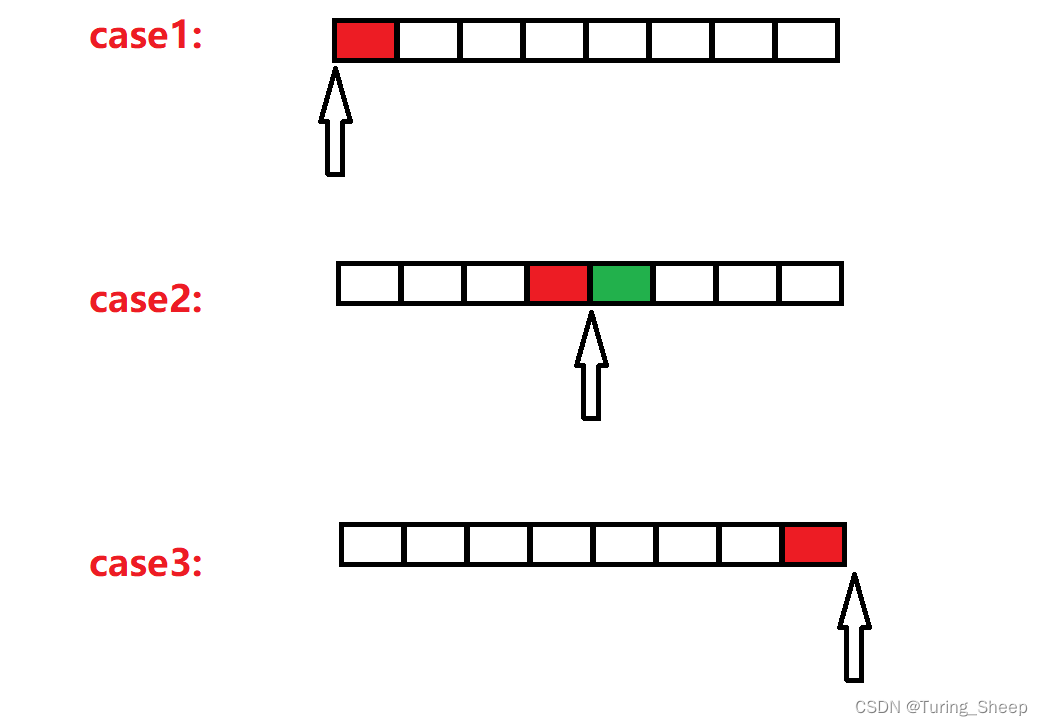
上图是一个$set$容器：

如果返回的是第一个元素的迭代器，那么容器中的第一个元素就是距离最近的。同理，如果返回了迭代器$end$，那么自然容器中的最后一个元素就是距离最近的。如果停在中间的位置：我们就需要考虑一下左右两个数字和我们当前的距离，因为右侧的数是第一个大于我们的数字，左侧的数是最后一个小于我们的数字。因此，我们需要在二者之间选一个距离最小的。

三、代码实现

#include<iostream>
#include<set>
#include<algorithm>
using namespace std;
int main()
{
    set<int>s;
    int n,sum=0;
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        auto it=s.lower_bound(x);
        if(s.empty())
        {
            sum+=x;
        }
        else
        {
            auto rit=it;
            auto lit=--it;
            int r=*rit;
            int l=*lit;
            if(rit==s.begin())
            {
                sum+=abs(r-x);
            }
            else if(rit==s.end())
            {
                sum+=abs(l-x);
            }
            else
            {
                sum+=min(abs(r-x),abs(l-x));
            }
        }
        s.insert(x);
    }
    cout<<sum;
    return 0;
}