B+树详解,一次就懂
⭐注意:不会直接讲 B+树的结构,会从最简单的二叉树开始讲起来。如果认真看完,我想你对树类型的数据结构的理解又上了一个新的台阶。
⭐如果有误,请大家指出。下文均是在B站学习的过程中,总结的笔记和心得体会
索引结构
MySQL索引是在 存储引擎层 实现的,不同的存储引擎层,有不同的索引结构,主要包含四种索引:
| 名称 | 简介 | |
|---|---|---|
| B+树索引 | 最常见的索引类型 | |
| Hash索引 | 底层是由 哈希表 实现 (⭐性能很强,但是!不支持范围查询) | |
| 空间索引(R-tree) | 是 MyISAM 引擎 的一个特殊索引类型,主要用于地理空间数据类型 | |
| 全文索引(Full-text) | 通过建立倒排索引方式,来快速匹配文档。 |
我们会从 二叉树 到 B+树
1、二叉树
-
二叉树,实际上就是一个简单的树形数据结构,本身没有什么意义。后来,规定了二叉树的插入顺序,让左子节点的元素永远小于右子节点。这种二叉树,可以快速的查询到某一个元素。
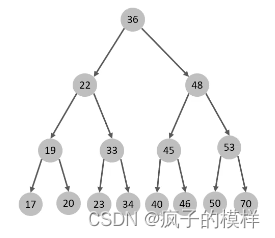
就这样, 二叉搜索树 诞生了。
-
在理想情况下,二叉树每多一层,可以存储的元素都增加一倍。那么 n个元素的二叉搜索树,对应的树高为log(n)。所以我们查找元素、插入元素的时间也为log(n)。
-
在不理想的情况下,每个节点元素顺序插入,所有的元素会线性排列,树形结构会退化成链表,就会形成如下图的结构,这样导致查询效率翻倍,为O(n) ———— 二叉搜索树不平衡的问题
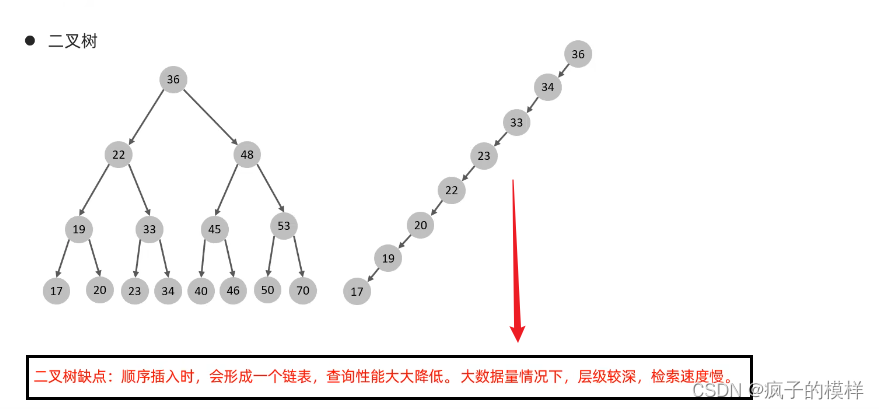
- (红黑树,自平衡的二叉树)
-
2、B 树
1. 多叉搜索树
-
上面我们知道了二叉搜索树,实际上多叉树和二叉树的区别就是: 多叉搜索树中的节点,可以存储多个元素。这样,导致多叉搜索树有多个分支
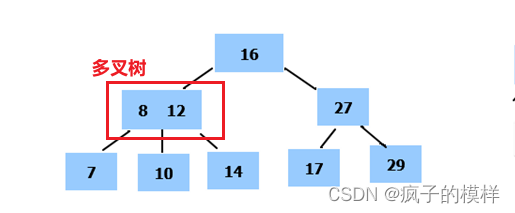
-
问题:二叉搜索树可以完成节点的高效增删改查,为啥会有多叉树的出现?
- 即 二叉搜索树不平衡的问题,当数量足够大时,树的深度会越深,查询效率就会越低。
- 在数据库存储中,树是一种常用的数据结构,其数据会存储在硬盘,那么每一次数据的读写都会在磁盘上进行读写,这一过程非常耗时。
- 树的深度越大,那么磁盘读写的次数越多,带来的IO开销也越大 (所以设计出了 B树,B树是多叉树的一种)
2. B 树
也叫 多路平衡查找树,实际上就是一颗多叉搜索树
B+ 树
和B 树类似,不过做了一些改变
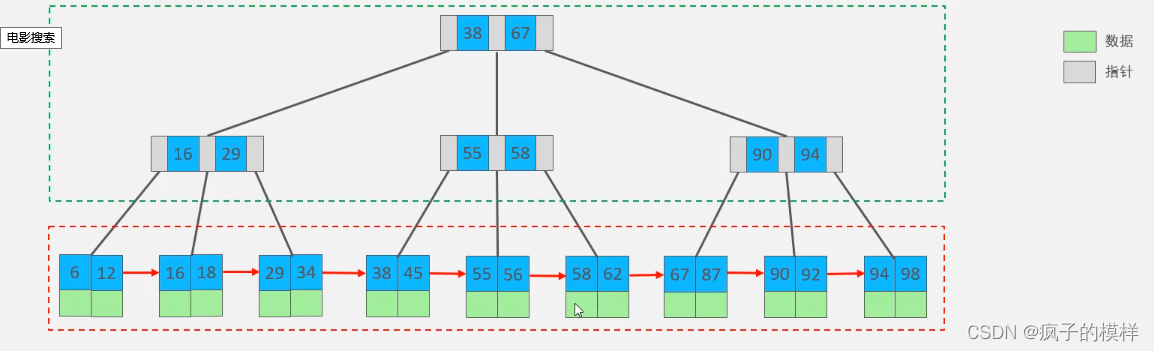
-
B+ 树 的特点 ( 从图中看 )
-
B+ 树的所有元素(数据),全部存放在叶子节点,即 所有的元素都会出现在叶子节点 。(B树 叶子节点和非叶子节点都存储数据)
- B树 的叶子节点、非叶子节点保存的是数据
- B+树 的非叶子节点是不保存数据的,只起到索引作用,它的叶子节点才保存数据。
-
非叶子节点,不存储数据,起到一个索引的作用
-
B+ 树 的数据结构中,叶子节点之间形成了单向链表。每一个节点的指针,通过叶子节点指向下一个元素。
-
B+ 树(MySQL)
MySQL中的 B+ 树,对经典的B+ 树结构进行了一个优化。在原基础上,叶子节点又增加了一条相邻叶子节点的指针。
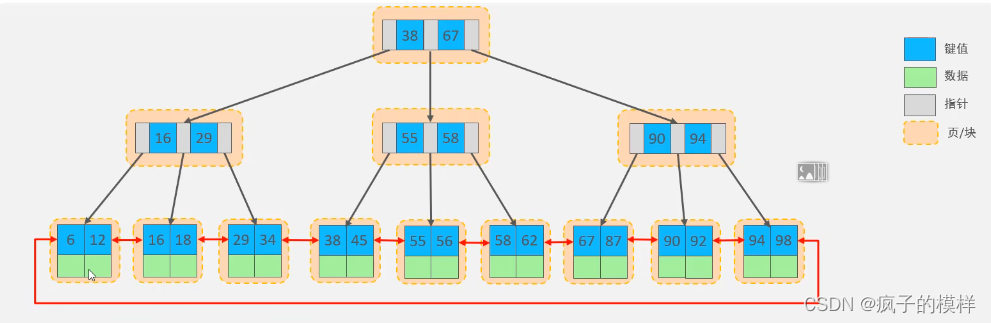
- 从图中可以看到,和 经典的B+树,结构大致一致。唯一不同的是,叶子节点之间形成了双向链表。
Hash索引

- 图详解:
- 看左边的表,我们 对 name 字段创建了 Hash索引,并查找 杨逍
- 首先对 name 采用 hash算法,得到hash值。通过生成的 hash值,映射到槽位 (杨逍,005)。
- 图中不难看到,005的位置,产生了 hash冲突
- 我们再对比 005槽位上链表的每一个元素,即可拿到值
-
特点
- 只能用于等值比较(=,in),不支持范围查询(between,>,< … )
- 无法利用索引完成排序操作
- 查询效率高(在索引中,查询小路是最高的)。在理想情况下,只需要检索一次(不发生Hash冲突的情况下)
-
Memory引擎,支持Hash索引,其他不支持。但是,InnoDB引擎 有自适应 hash 功能,会根据查询条件 自动的将 B+树索引,构建为Hash索引
