【数据结构】手撕八大排序算法
作者:一个喜欢猫咪的的程序员
专栏:《数据结构》
喜欢的话:世间因为少年的挺身而出,而更加瑰丽。 ——《人民日报》
目录
1.排序的概念:
2.八大排序的思路及其细节
2.1直接插入排序
2.2希尔排序
2.3选择排序:
2.4堆排序
2.5冒泡排序
2.6快速排序:
2.6.1hoare版本(递归版本)
2.6.2三数取中
2.6.3挖坑法
2.6.4前后指针法:
2.6.5非递归写法:
2.7归并排序
2.7.1递归写法:
2.7.2非递归写法:
2.8计数排序

1.排序的概念:
排序就是把集合中的元素按照一定的次序排序在一起。一般来说有升序排列和降序排列2种排序,在算法中有八大基本排序:

算法的优良主要从4个方面进行评测:
- 1.时间复杂度
- 2.空间复杂度
- 3.适用场景
- 4.稳定性
2.八大排序的思路及其细节
2.1直接插入排序
动图演示:
当前n-1个已是有序的情况下,将第n个元素插入进去排序,插入到顺序正确的位置。
将此过程一直重复的话可以可以完成上图的情况。(以数组a为例,来观察一下各个过程)
int a[] = {9,1,2,5,7,4,8,6,3,5};
思路:
用一个变量end=i,利用tmp记录下end位置的下一个位置a[end+1]的值,如果a[end]>tmp,a[end]=tmp然后end--。最后将tmp的值赋给end+1的位置。
考虑极端情况:
当数组有n个数时,下标最大值为n-1
当end=n-1时,end+1=n(此时造成了越界)
void InsertSort(int* a, int n)
{//插入排序
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end+1] = tmp;//防止end=-1
}
}时间复杂度: O(N^2) 空间复杂度:O ( 1 )
2.2希尔排序
对插入排序的时间复杂度进行分析,得出了以下结论:
- 普通插入排序的时间复杂度最坏情况下为O(N2),此时待排序列为逆序,或者说接近逆序。
- 普通插入排序的时间复杂度最好情况下为O(N),此时待排序列为升序,或者说接近升序。
动图演示:
待排序列先进行一次预排序,让待排序列变为接近有序的(接近需要的顺序),然后再进行一次直接插入排序。
因为直接插入排序前的待排序列已是接近有序的情况了,因此时间复杂度为O(N),只要控制预排序阶段的时间复杂度不超过O(N^2),那么整体的时间复杂度就比直接插入排序的时间复杂度低了。

希尔排序法又称缩小增量法。希尔排序法的基本思想是:
设定一个gap=n/2,将相距gap位置的两个数作比较,如果前面的小于后面交换以此循环
问题:为什么gap=n/2?
answer:gap越大,数据挪动得越快;gap越小,数据挪动得越慢。前期让gap较大,可以让数据更快得移动到自己对应的位置附近,减少挪动次数。
注:一般情况下,取序列的一半作为增量,然后依次减半,直到增量为1(也可自己设置)。
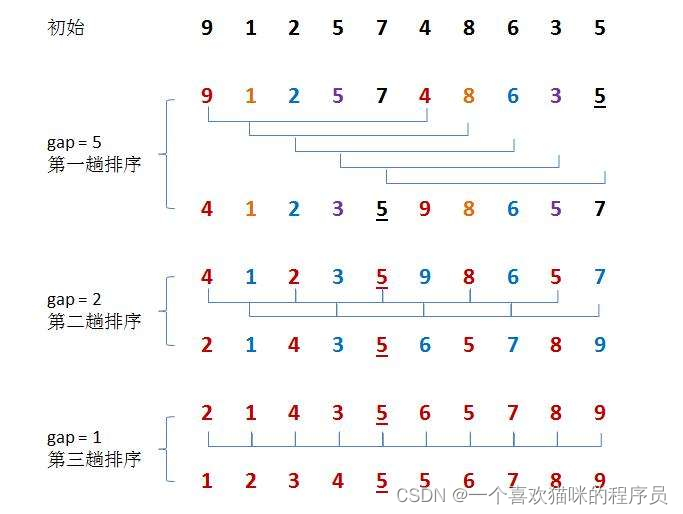
思路:
单趟排序:当a[end]>a[end+gap]时,将end的值赋给end+gap后end-=gap,在end<0时退出循环
当有n个数时,因为比较是相距gap距离的两个数比较,因此循环次数要小于n-gap次
gap=n每次取半直到最终取到gap=1时,每次取半都是一次一次单趟排序

void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap/ 2;
for (int i = 0; i < n - gap; i++)//i++并排运算
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
//Swap(&a[end], &a[end + gap]);
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;//防止end<0
}
}
}希尔排序详细的时间复杂度和空间复杂度:
《数据结构(C语言版)》--- 严蔚敏

《数据结构-用面相对象方法与C++描述》--- 殷人昆

时间复杂度:O ( NlogN ) 空间复杂度:O ( 1 )
平均时间复杂度:O ( N^ 1.3 )
2.3选择排序:
动图演示:

思路:
设两个下标begin和end,begin初始化为0,end初始化为n-1
设置最大值和最小值的下标让他们指向begin和end
当a[i]的值比a[begin]小,更新min的值,当a[i]的值比a[begin]大,更新max的值
循环走完后确认了最小值的下标,将a[begin]和a[min]进行交换,以及a[end]和a[max交换]
极端情况:
当最大值为数组的第一个时,max=min
时间复杂度:O(N^2) 空间复杂度:O(1)
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin;
int maxi = end;
for (int i = begin+1; i <=end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[mini], &a[begin]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[maxi], &a[end]);
begin++;
end--;
}
}2.4堆排序
堆排序:(以小堆为例)
堆的分类:
1.升序or降序
2.大堆or小堆
void test2()
{//堆排序
int array[] = { 27,15,19,18,28,34,65,49,25,37 };
Heapsort(array, sizeof(array) / sizeof(array[0]));
for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++)
{
printf("%d ", array[i]);
}
printf("\n");
}Heapsort函数(堆排序):
int array[] = { 27,15,19,18,28,34,65,49,25,37 };
需将这个数组进行大堆排列,分为两种调整形式:向上调整和向下调整。
向上调整和向下调整的思想可以参考我的例外一篇博客:http://t.csdn.cn/UD52X
void Ajustup(HPDataType*a, int child)
{//N*logN
assert(a);
//int child = n - 1;
while (child > 0)
{
int parent = (child - 1) / 2;
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
}
else
{
break;
}
}
}
void Ajustdown(HPDataType* a, int n,int parent)
{//O(N)
assert(a);
int child = 2 * parent+1;
while (child<n)
{
if (child + 1 < n && a[child] < a[child + 1])// <假设左子树大
{
child++;
}
if (a[child] > a[parent])//>大堆,<为小堆
{
Swap(&a[child], &a[parent]);
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}向上调整和向下调整具体的时间复杂度是多少呢?
向下调整具体的时间复杂度:
假设树高为h
第h层,有2^(h-1)个节点,需要向下调整0次(直接不算,从第h-1层开始算)。
第h-1层,有2^(h-2)个节点,需要向下调整1层。
第h-2层,有2^(h-3)个节点,需要向下调整2层。
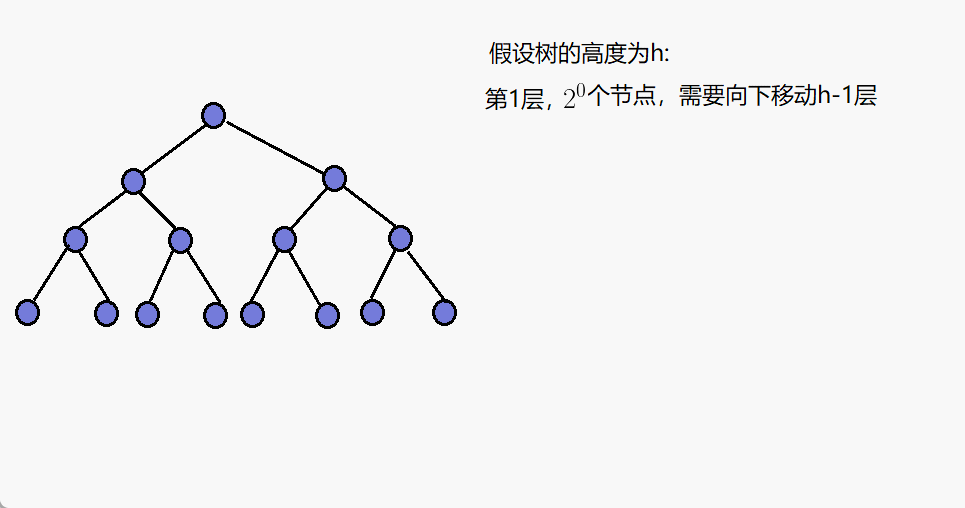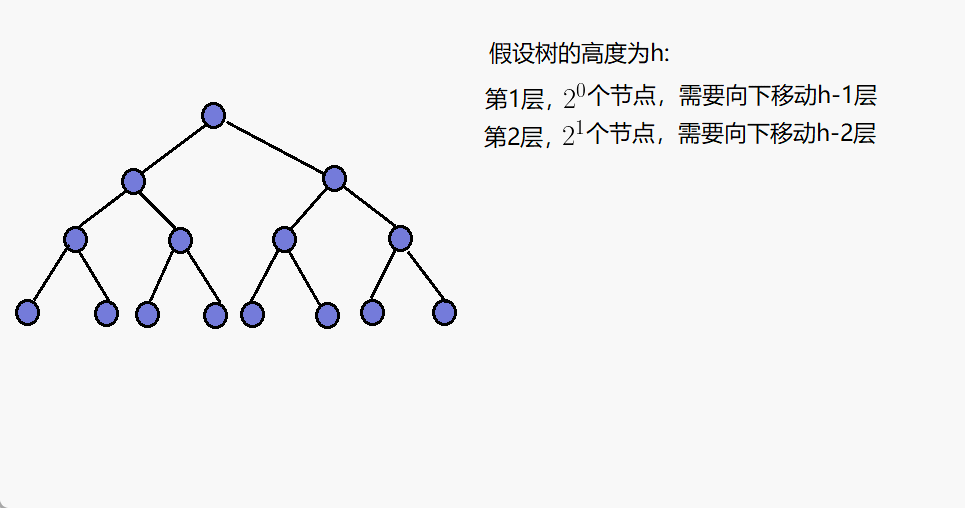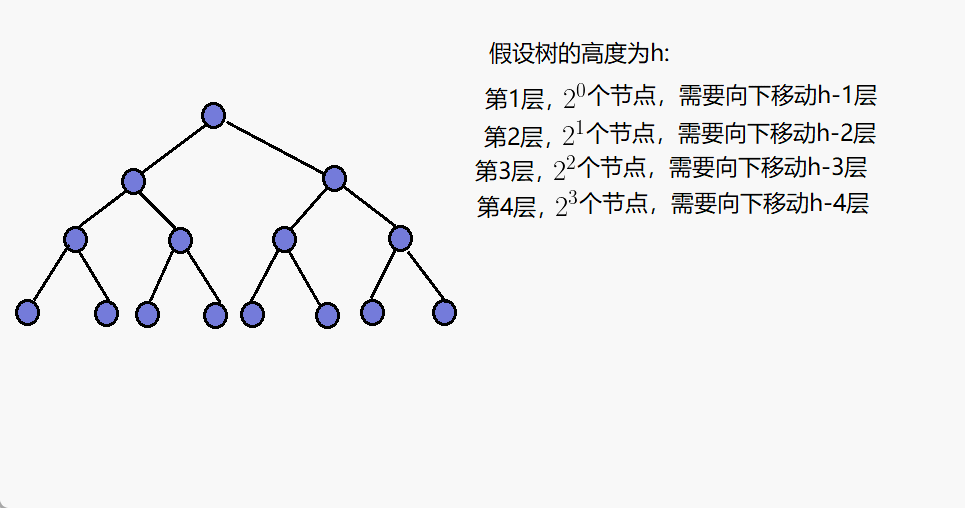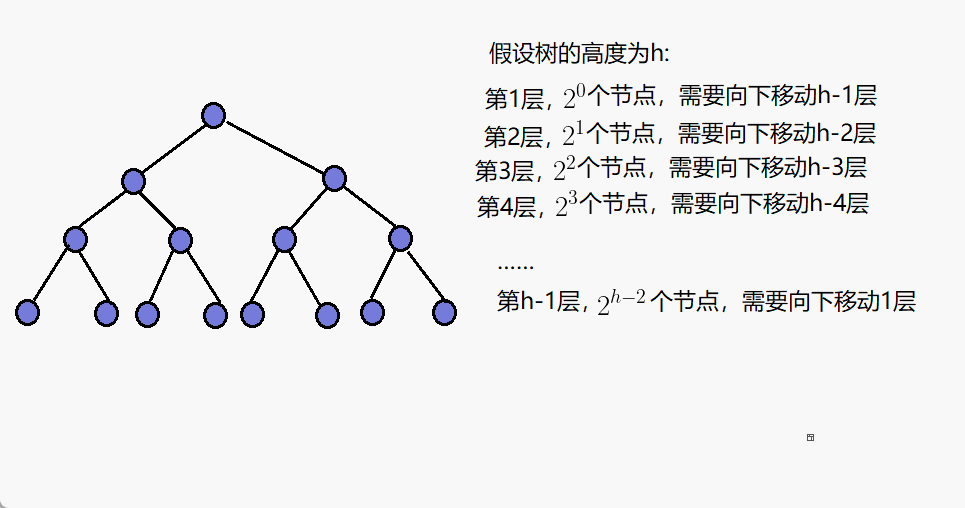
......
第4层,有2^3个节点,需要向下调整h-4层。
第3层,有2^2个节点,需要向下调整h-3层。
第2层,有2^1个节点,需要向下调整h-2层。
第1层,有2^0个节点,需要向下调整h-1层。
当h高的次数,最多调整层数为:
F(h)=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+...+2^(h-3)*2+2^(h-2)*1+2^(h-1)*0 ——①
2*F(h)=2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+...+2^(h-2)*2+2^(h-1)*1+2^(h)*0 ——②
有错位相减②-①可得:
F(h)=-2^0*(h-1)+2^1+2^2+....+2^(h-2)+2^(h-1)
F(h)=2^h-1-h ——③
当树高为h时,节点总个数N为:
N=2^0+2^1+...+2^(h-2)+2^(h-1)
N=2^h-1 ——④
有④可得:h=log(N+1) ——⑤
综合③④⑤可得:
F(N)=N-log(N+1)
- 因此时间复杂度为O(N)
向上调整具体的时间复杂度:
在一层,需要向上调整0次第二层,向上调整1次
第三层,向上调整2次
...
第h-1层,向上调整h-2次
第h层,向上调整h-1次
F(h)=2^1*1+2^2*2+....+2^(h-1)*(h-1)。
由错位相减可得:
F(N)=2N(1-log(N+1))。
时间复杂度为O(N*logN)
如何实现堆排序
显然向下调整优于向上调整。
先利用Ajustdown排序好数组,然后再用交换Ajustdown实现小堆。
void Heapsort(int*a,int n)//堆排序
{//向上调整
for (int i = 1; i <n; i++)
{
Ajustup(a, i);
}
//向下调整
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
Ajustdown(a, n, i);
}
int end = n - 1;
while (end>0)
{
Swap(&a[0], &a[end]);
Ajustdown(a, end, 0);
end--;
}
//N*logN
}
void test2()
{//堆排序
int array[] = { 27,15,19,18,28,34,65,49,25,37 };
Heapsort(array, sizeof(array) / sizeof(array[0]));
for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++)
{
printf("%d ", array[i]);
}
printf("\n");
}2.5冒泡排序
动图演示:
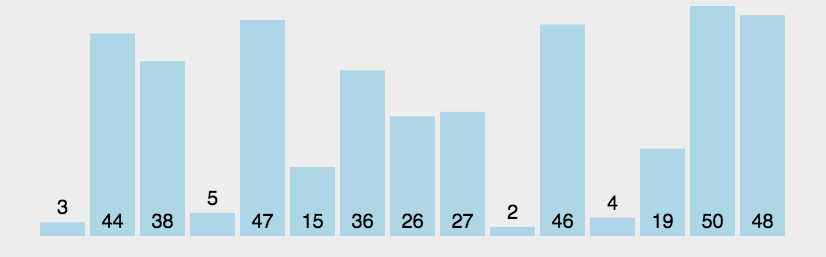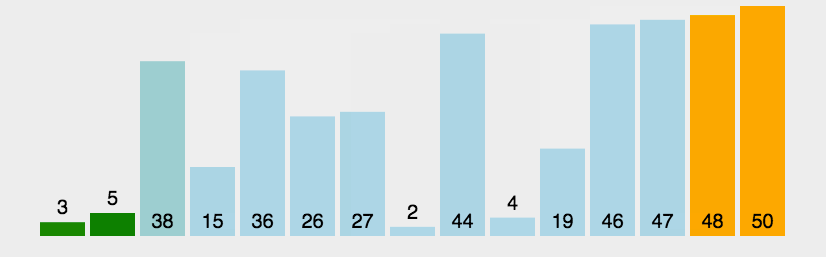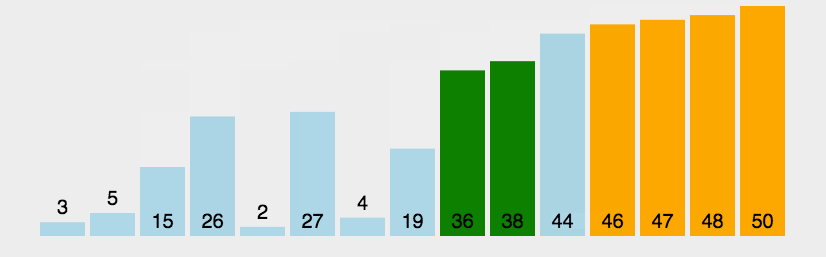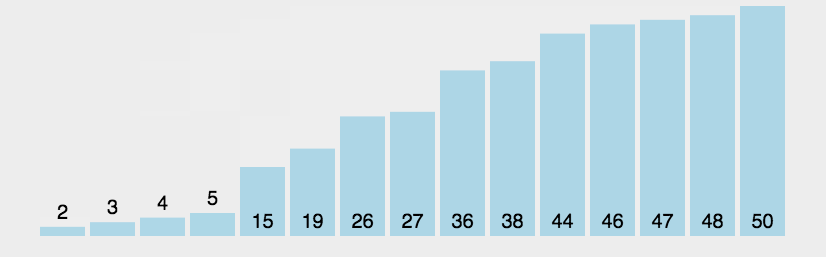
代码:
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
for (int i = 1; i < n - j; i++)
{
if (a[i] < a[i - 1])
{
Swap(&a[i],& a[i - 1]);
}
}
}
}时间复杂度:O(N^2) 空间复杂度:O(1)
2.6快速排序:
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
快速排序有三种写法:
1.hoare版本
2.挖坑法
3.前后指针法
以及优化:
1.三数取中
2.6.1hoare版本(递归版本)
动图演示:
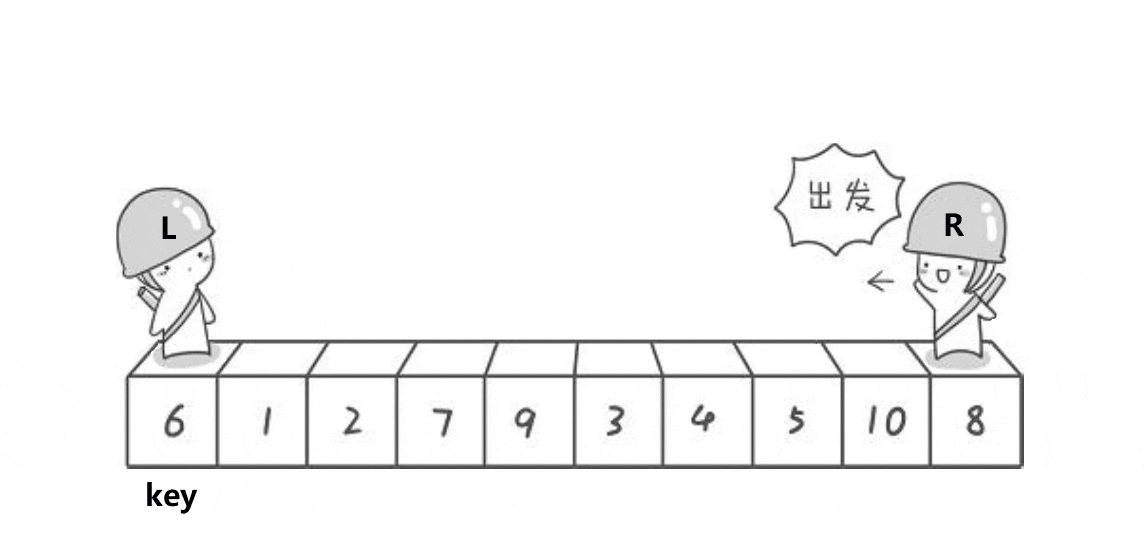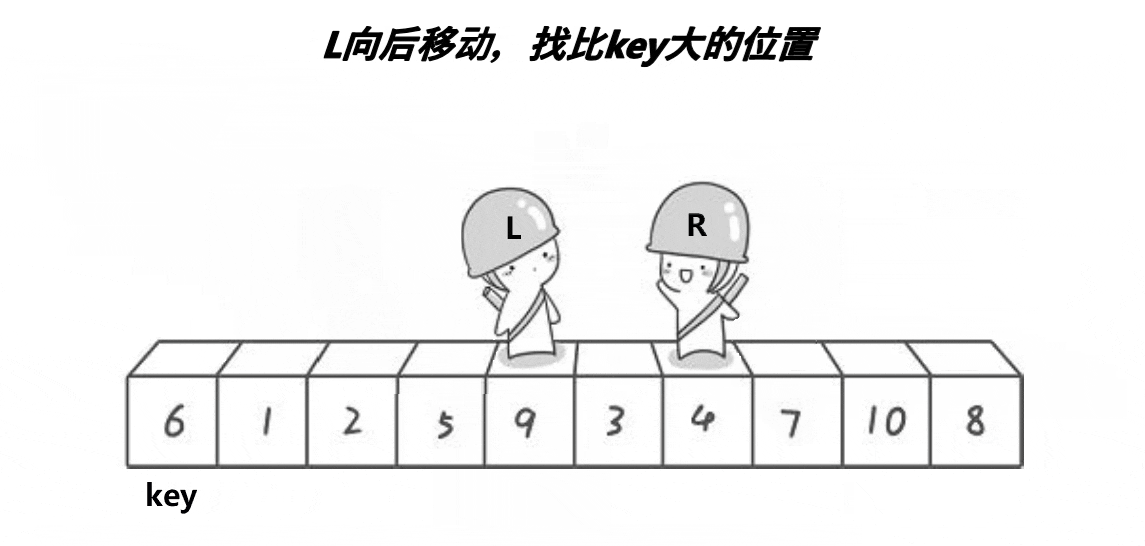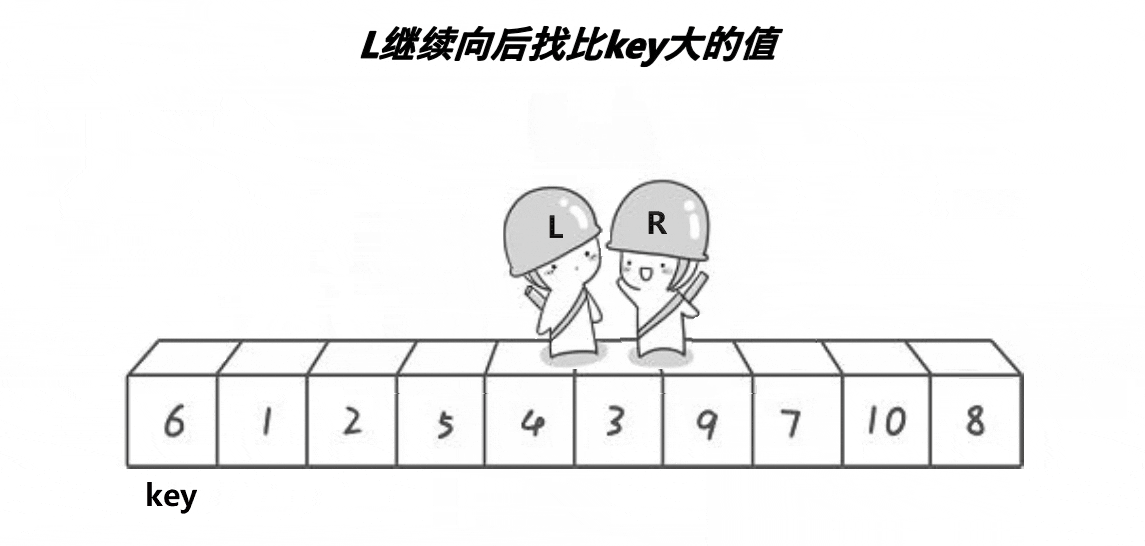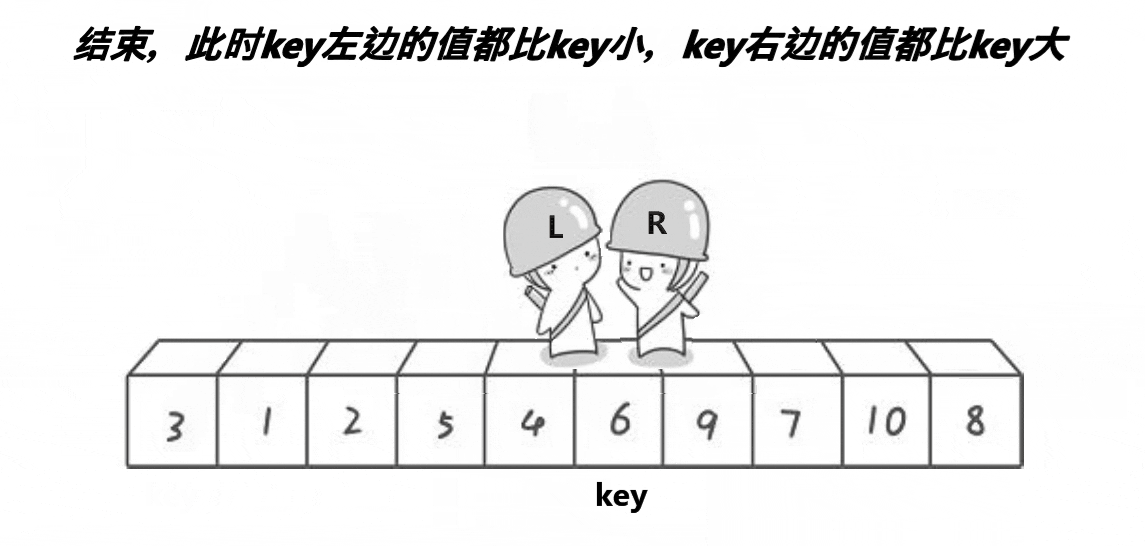
hoare版本思路:
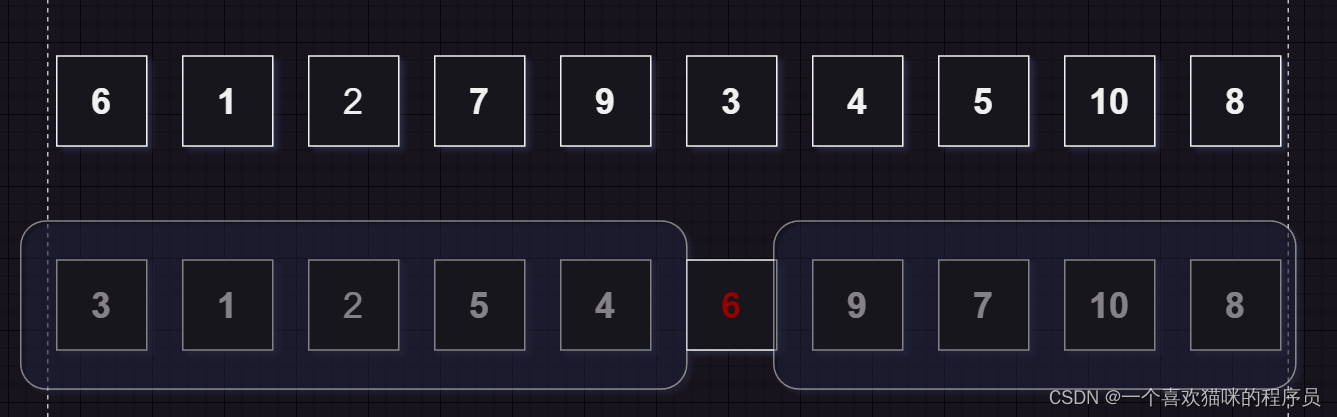
单趟排序,key一般选最左边或者最右边
当key为最左边,右边找小,左边找大,然后交换继续,相遇停止,相遇的值跟key交换
当key为最右边相反
当左区间有序,右区间有序那整体就ok了,如果左右区间不有序,左右区间就是单趟的子问题
当区间只有一个值,就不排了,返回
问题:为什么是key为最左边时,右边先走,最右边做key时,左边先走
answer:左边做key,右边先走,可以保证相遇位置比key要小
此时有两种情况:
1.相遇,left是停着(一定>=key),right向后走,相遇的位置是left的位置
2.相遇,right是停着(一定<=key),left向前走,相遇的位置是right的位置
单趟有两个意义
1.分割出左右区间,左比key小,右比key大
2.key到了正确位置(排序后的最终位置)
key以后不用变了,到了正确位置
代码:
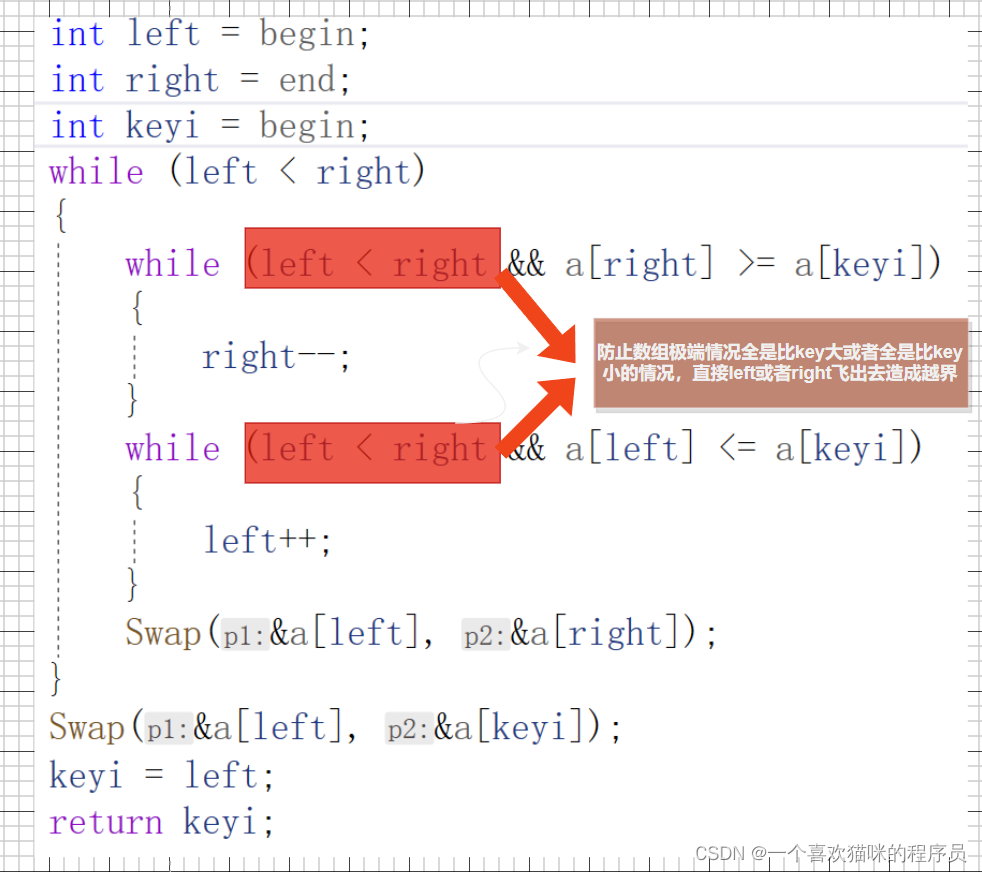
int Partsort1(int* a, int begin, int end)
{//hoare版本
int mid = GetMidIndex(a, begin, end);
Swap(&a[mid], &a[begin]);
int left = begin;
int right = end;
int keyi = begin;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
right--;
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end-begin+1 < 10)
{
InsertSort(a + begin, end - begin + 1);
}
else
{
int keyi=Partsort1(a, begin, end);
//int keyi=Partsort2(a, begin, end);
//int keyi = Partsort3(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}时间复杂度:O(NlogN)
2.6.2三数取中
每次排序都会将数组分为三个部分:
【left-key-1】【key】【keyi+1-right】
在理想情况下,我们每次进行完单趟排序后,key的左序列与右序列的长度都相同:
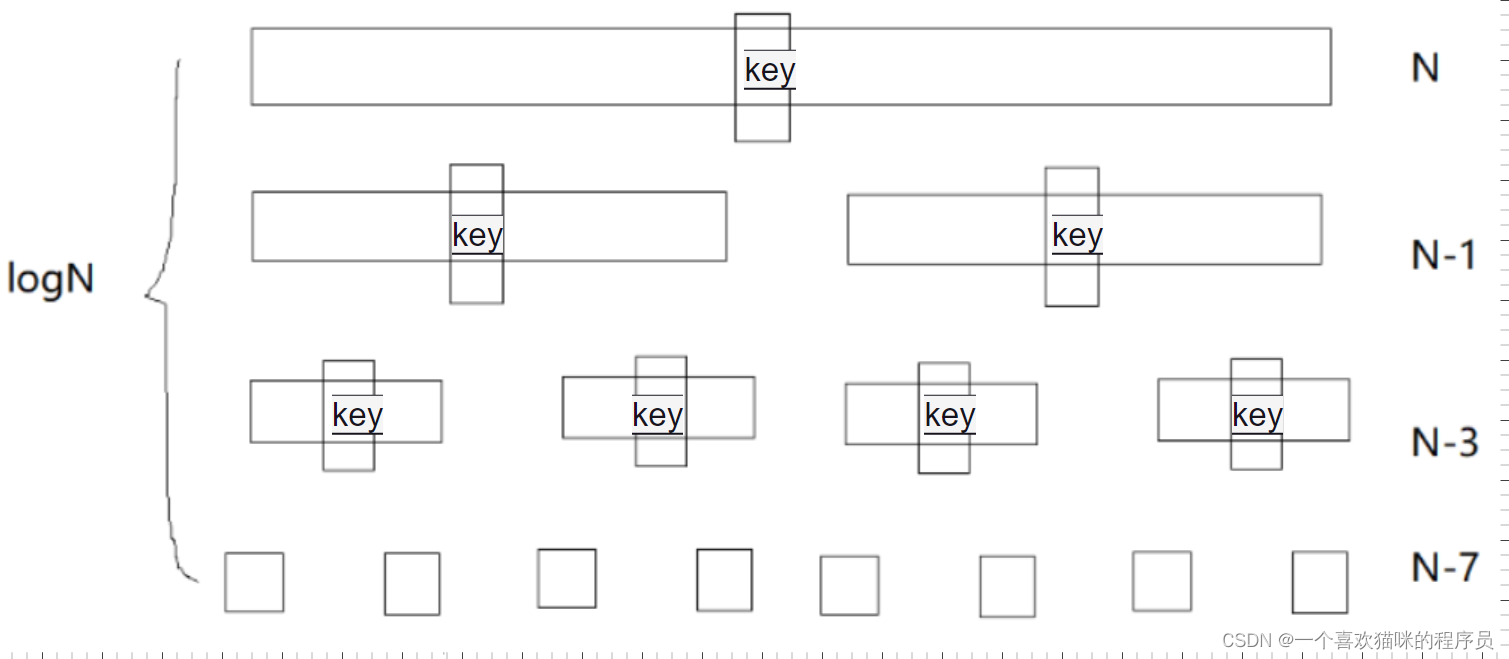
若每趟排序所选的key都正好是该序列的中间值,即单趟排序结束后key位于序列正中间,那么快速排序的时间复杂度就是O(NlogN)。
但事实上可能会遇到极端情况:就是我们每次取到的都是最大值或者最小值,那么快排的时间复杂度达到最低O(N^2)
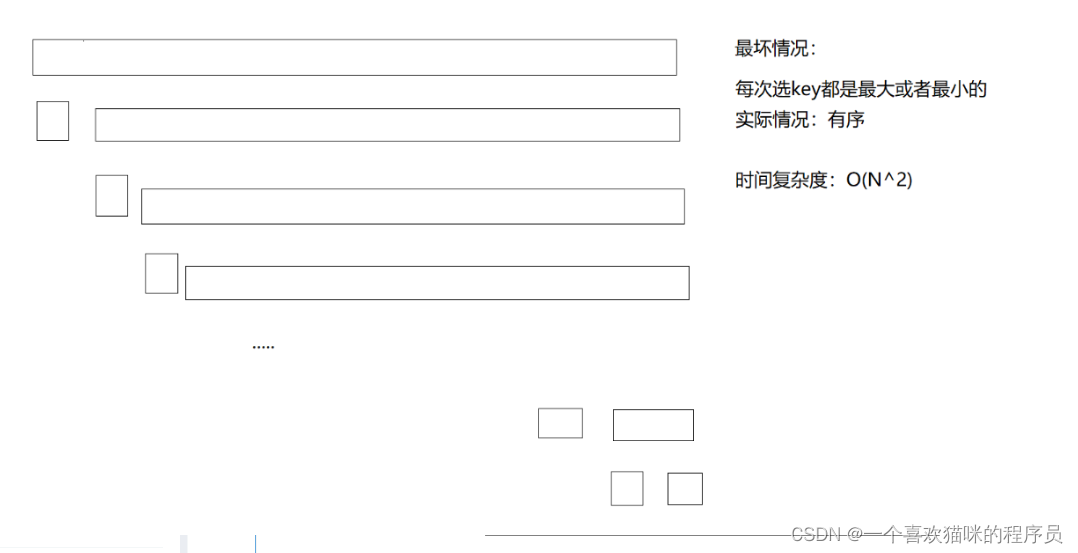
可以看到,这种情况下,快速排序的时间复杂度退化为O(N^2)。其实,对快速排序效率影响最大的就是选取的key,若选取的key越接近中间位置,则则效率越高。
为了避免这种极端情况的发生,于是出现了三数取中:
三数取中,当中的三数指的是:最左边的数、最右边的数以及中间位置的数。三数取中就是取这三个数当中,值的大小居中的那个数作为该趟排序的key。这就确保了我们所选取的数不会是序列中的最大或是最小值了。
代码:
int GetMidIndex(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] > a[end])//a[mid]>a[end]的前提下
{
return begin;
}
else//a[mid]>a[end]&&a[begin] < a[end]的前提下
{
return end;
}
}
else//a[begin] > a[mid]
{
if (a[end] < a[mid])
{
return mid;
}
else if (a[begin] > a[end])//a[end] > a[mid]
{
return end;
}
else//a[end] > a[mid]&&a[begin] < a[end]
{
return begin;
}
}
}2.6.3挖坑法
动图演示:
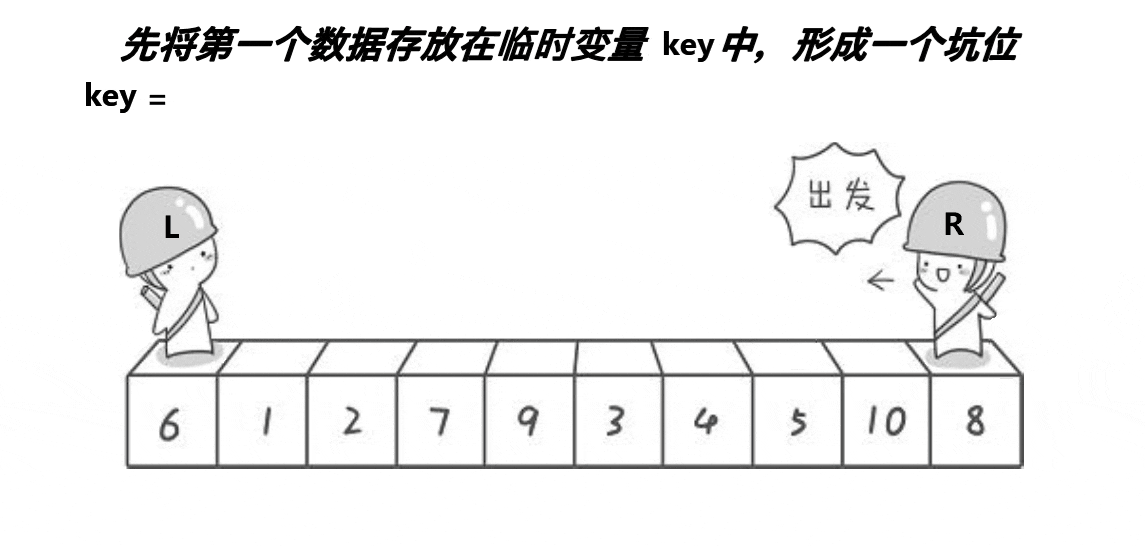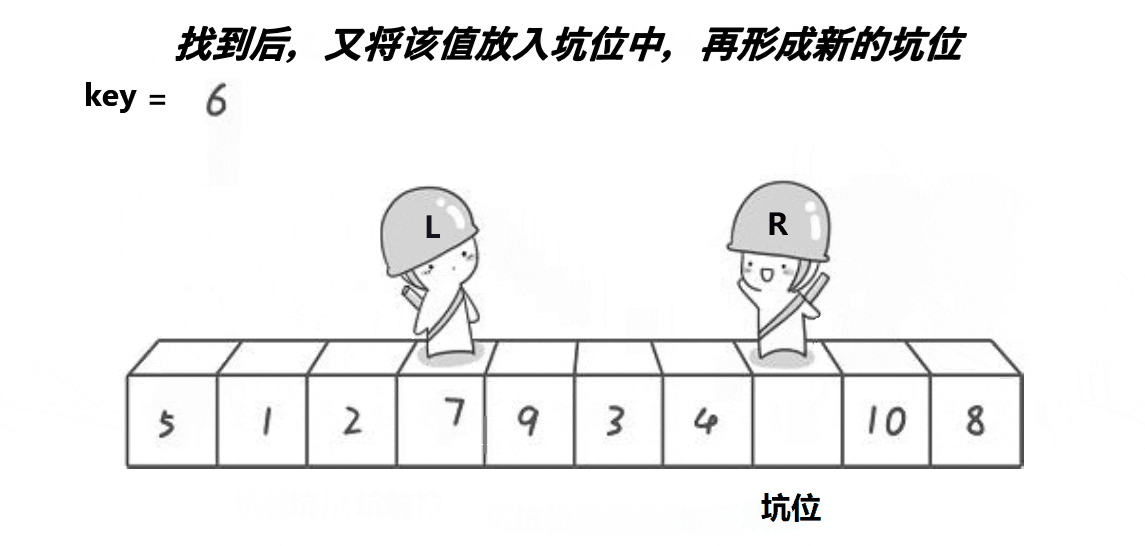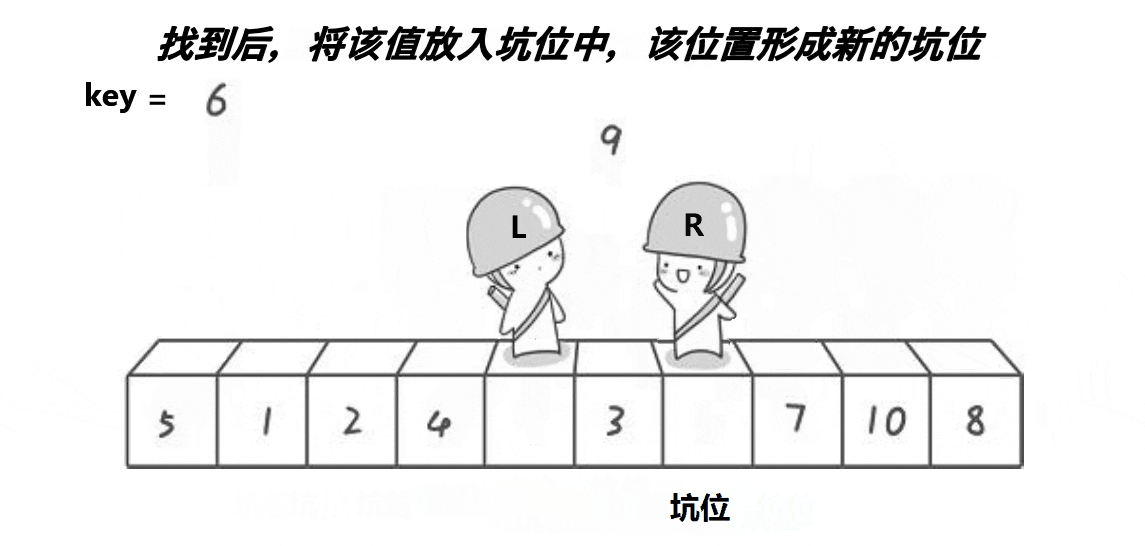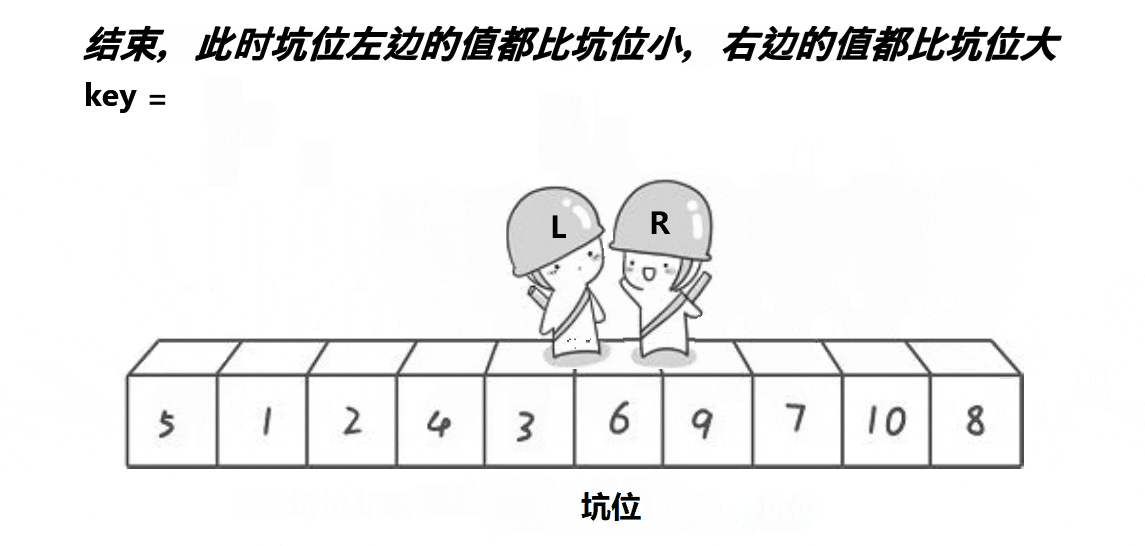
思路:
将一开始的left保存起来,然后左边 空出来一个坑,右边先走,右找大,然后将右边的值的数据填进去,找到的位为坑,左边找小将右边的坑填进去,最后一定会在坑的位置相遇
代码:
int Partsort2(int* a, int begin, int end)
{//挖坑法
int mid = GetMidIndex(a, begin, end);
Swap(&a[mid], &a[begin]);
int left = begin;
int right = end;
int keyi = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= keyi)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= keyi)
{
left++;
}
a[hole]=a[left];
hole = left;
}
a[hole] = keyi;
keyi = left;
return hole;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end-begin+1 < 10)
{
InsertSort(a + begin, end - begin + 1);
}
else
{
//int keyi=Partsort1(a, begin, end);
int keyi=Partsort2(a, begin, end);
//int keyi = Partsort3(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}时间复杂度:O(NlogN)
2.6.4前后指针法:
动图演示:
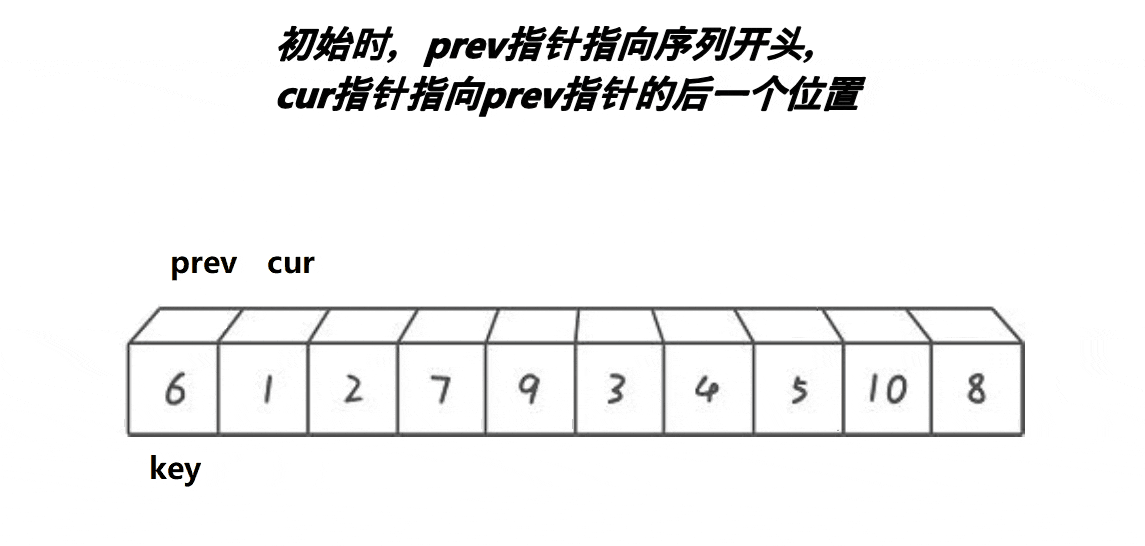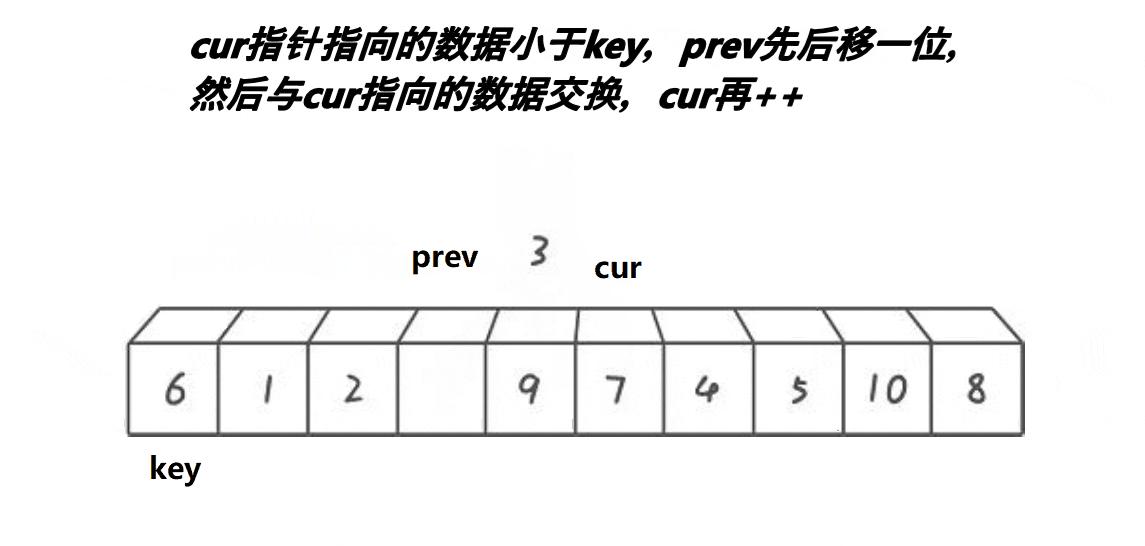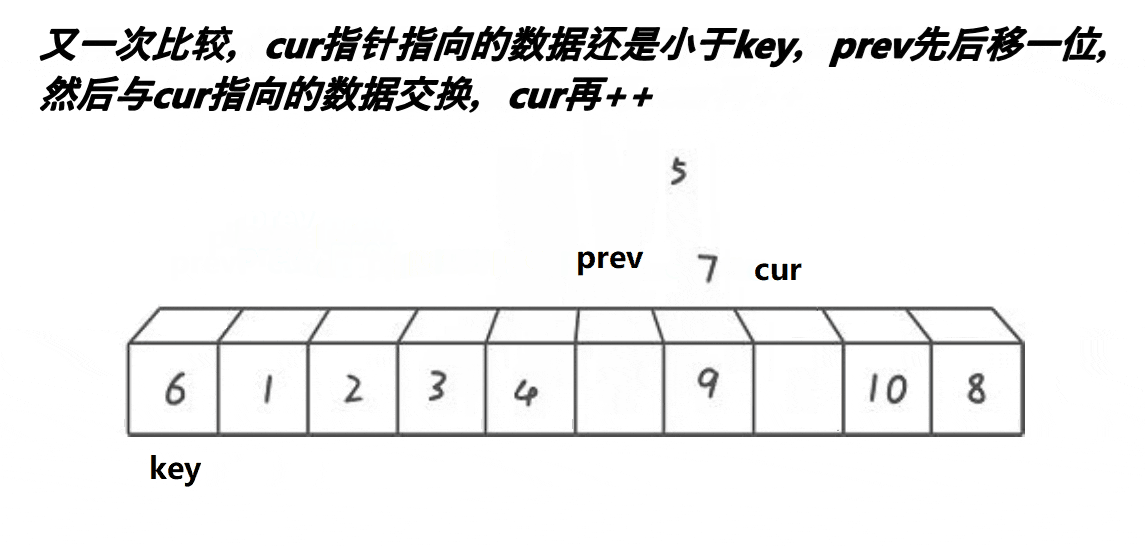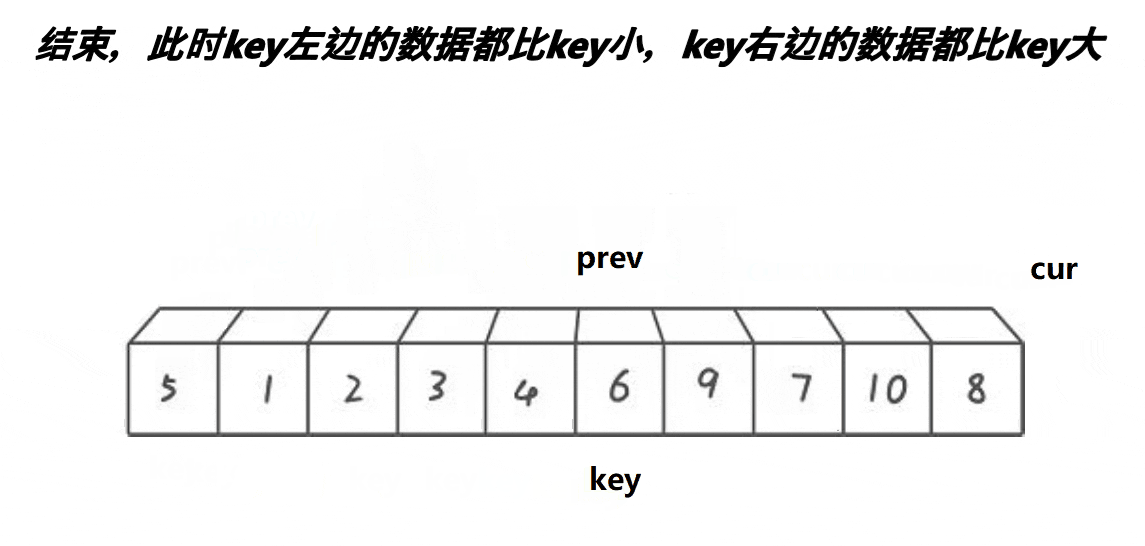
思路:
1、cur找比key小,找到后停下来
2、++prev, 交换prev位置和cur位置的值
代码:
int Partsort3(int* a, int begin, int end)
{
int prev = begin;
int cur = begin + 1;
int keyi = begin;
while (cur<=end)
{
/*if (a[cur] < a[keyi])
{
Swap(&a[++prev], &a[cur]);
}*/
if (a[cur] < a[keyi]&&++prev!=cur)
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end-begin+1 < 10)
{
InsertSort(a + begin, end - begin + 1);
}
else
{
/*int keyi=Partsort1(a, begin, end);
int keyi=Partsort2(a, begin, end);*/
int keyi = Partsort3(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}时间复杂度:O(NlogN)
2.6.5非递归写法:
思路:
通过非递归的方式实现递归的情况的话,递归从底层是先排左边再排右边因此类推,因此写非递归我们从顶层到底层就需要反过来。
借助栈的内存结构让先入的后出,所以要先压begin再压end,取出来的话就是先出右再出左
再先排右边再排左边。
代码:
void QuickSortNonR(int* a, int begin, int end)
{//非递归
ST st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st, end);
while (!StackEmpty(&st))
{
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
int keyi = Partsort3(a, left, right);//单趟排序
if (keyi + 1 < right)
{
StackPush(&st, keyi+1);
StackPush(&st, right);
}
if (left < keyi-1)
{
StackPush(&st, left);
StackPush(&st, keyi - 1);
}
}
StackDestory(&st);
}2.7归并排序
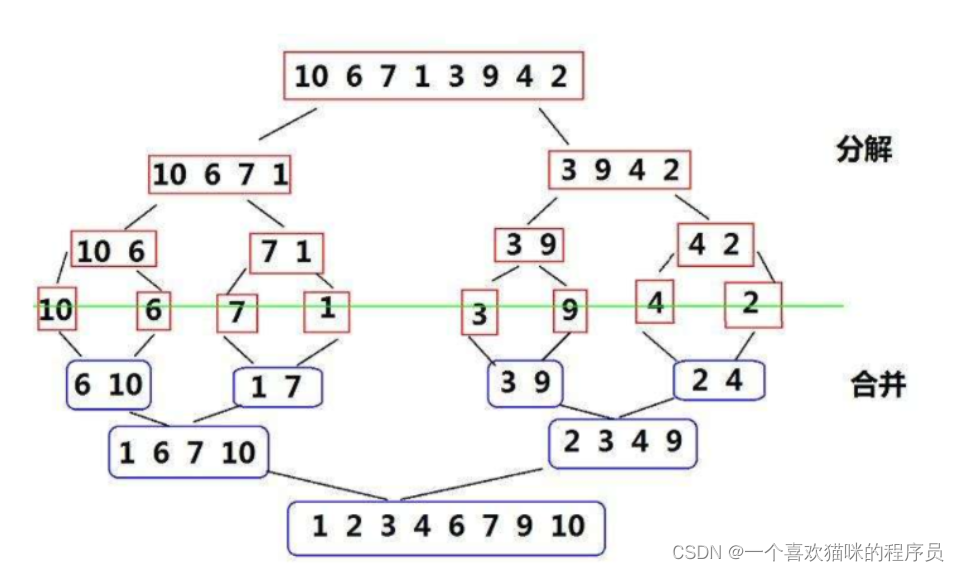
2.7.1递归写法:
动图讲解:
思路:
将两端有序序列取各种较小的值比较排序成一个有序序列。
代码:
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, mid+1, end, tmp);
_MergeSort(a, begin, mid, tmp);
int begin1 = begin;
int end1 = mid;
int begin2 = mid+1;
int end2 = end;
int i = begin;
while (begin1<=end1&&begin2<=end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
_MergeSort(a, 0, n-1, tmp);
free(tmp);
tmp = NULL;
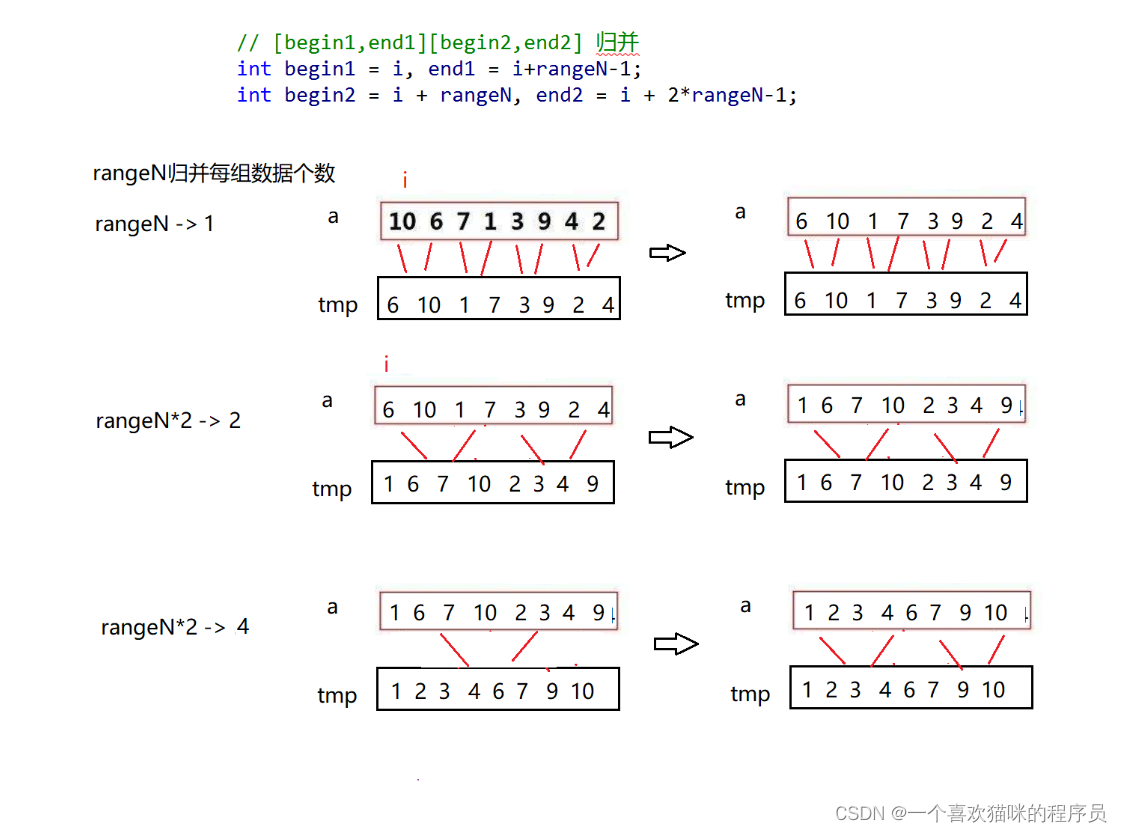
}2.7.2非递归写法:
极端情况:
越界有三种情况
1.end1越界 begin2越界end2越界
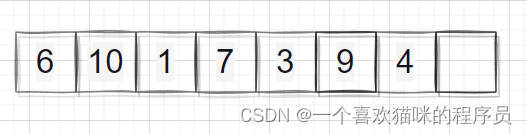
2.begin2越界end2越界
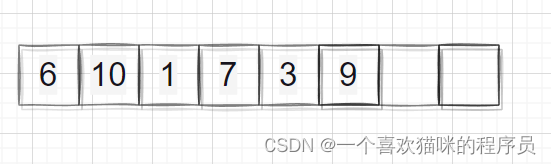
3.end2越界
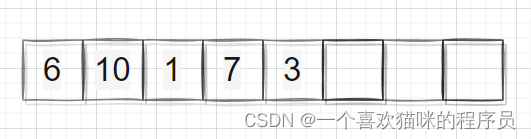
整体拷贝的话会有覆盖丢失
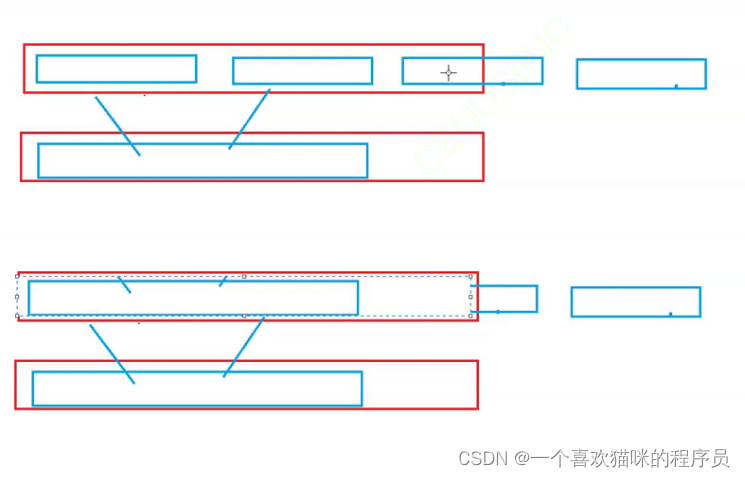 代码:
代码:
void MergeSortNonrR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int RangN = 1;
while (RangN < n)
{
for (int i = 0; i < n; i += 2 * RangN)
{
int begin1 = i;
int end1 = i + RangN - 1;
int begin2 = i + RangN;
int end2 = i + 2 * RangN - 1;
int j = i;
if (end1>=n)// 修正区间 ->拷贝数据 归并完了整体拷贝 or 归并每组拷贝
{
end1 = n - 1;
begin2 = n;// 不存在区间
end2 = n - 1;
}
else if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
else if(end2>=n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
RangN *= 2;
}
free(tmp);
tmp = NULL;
}时间复杂度:O(NlogN) 空间复杂度:O(N)
2.8计数排序
思路:
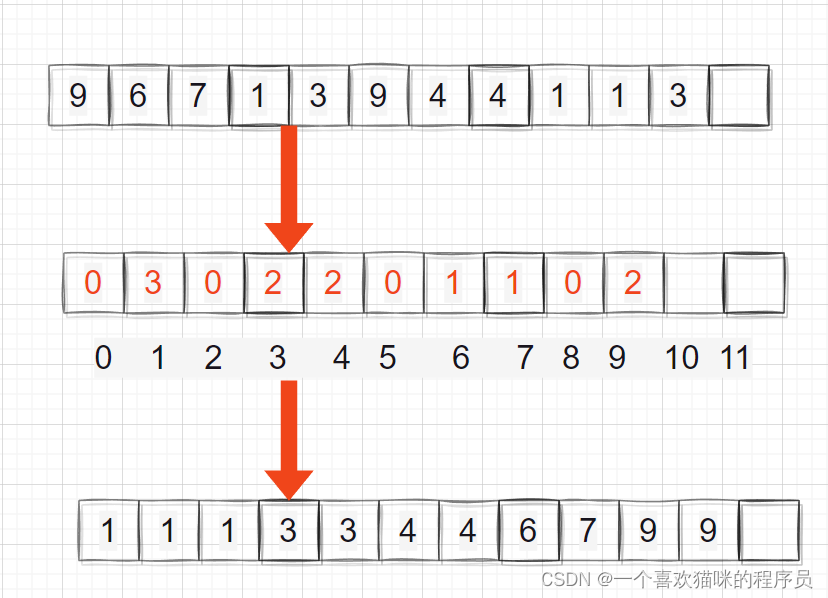
绝对映射:count数组中下标为i的位置记录的是arr数组中数字i出现的次数。
相对映射:count数组中下标为i的位置记录的是arr数组中数字min+i出现的次数。
代码:
void CountSort(int* a, int n)
{
int min = a[0];
int max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;
int* CoutA = (int*)calloc(range, sizeof(int));
if (CoutA == NULL)
{
perror("calloc fail");
exit(-1);
}
for (int i = 0; i < n; i++)
{
CoutA[a[i] - min]++;
}
int k = 0;
for (int i = 0; i < range; i++)
{
while (CoutA[i]--)
{
a[k++] = i + min;
}
}
free(CoutA);
}时间复杂度:O(N+range) 空间复杂度:O(range)