当前位置：首页 > news >正文

算法leetcode｜31. 下一个排列（rust重拳出击）

news 来源：原创 2024/11/17 5:52:45

文章目录

31. 下一个排列：
- 样例 1：
- 样例 2：
- 样例 3：
- 提示：
分析：
题解：
- rust
- go
- c++
- c
- python
- java

31. 下一个排列：

整数数组的一个排列就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

样例 1：

输入：
	nums = [1,2,3]
	
输出：
	[1,3,2]

样例 2：

输入：
	nums = [3,2,1]
	
输出：
	[1,2,3]

样例 3：

输入：
	nums = [1,1,5]
	
输出：
	[1,5,1]

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 100

分析：

面对这道算法题目，二当家的陷入了沉思。
关键是要找到下一个排列的一般性规律。

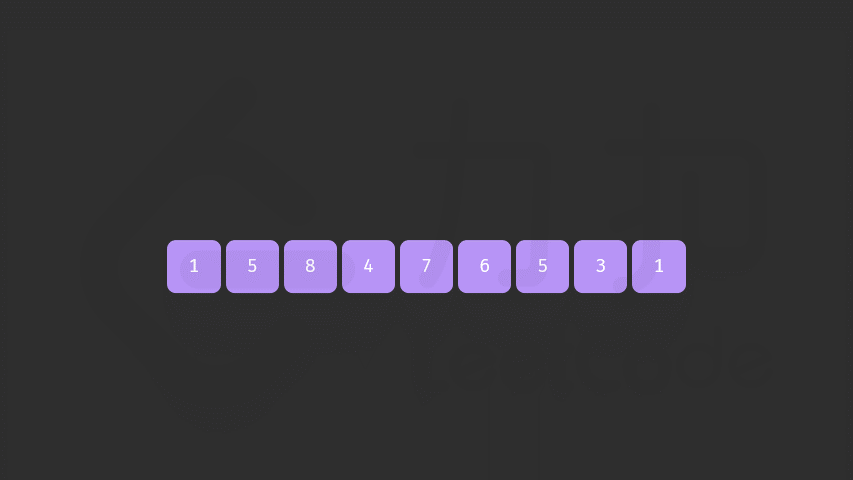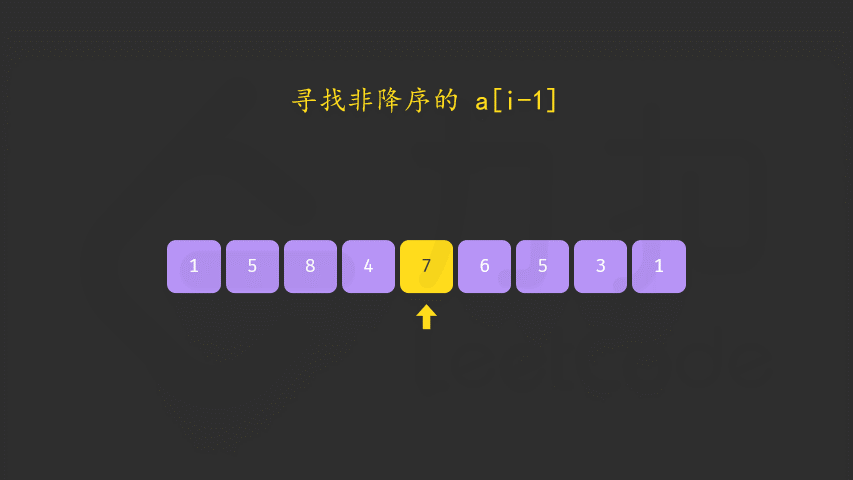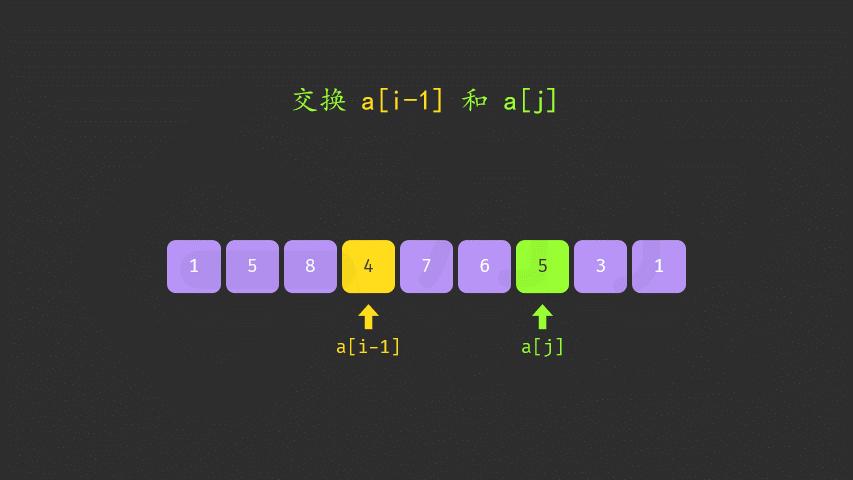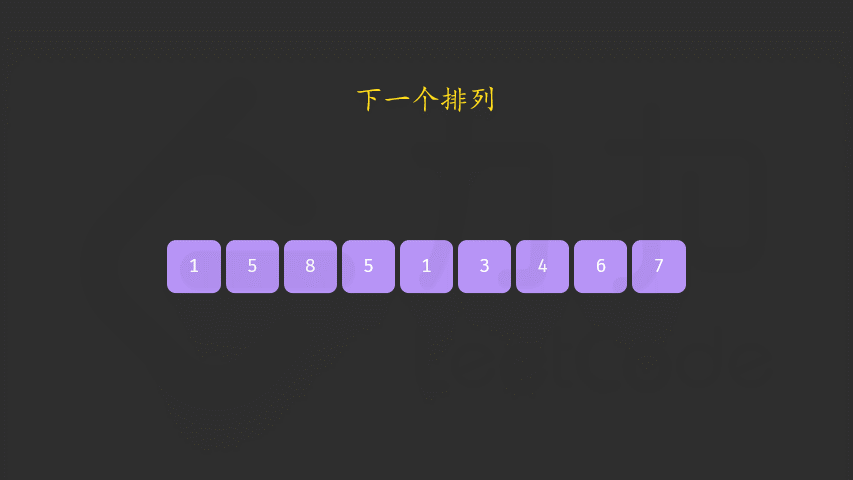
首先从后向前查找第一个顺序对 (i,i+1)，满足 a[i]<a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。
如果找到了顺序对，那么在区间 [i+1,n) 中从后向前查找第一个元素 j 满足 a[i]<a[j]。这样「较大数」即为 a[j]。
交换 a[i] 与 a[j]，此时可以证明区间 [i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序，而无需对该区间进行排序。

题解：

rust

impl Solution {
    pub fn next_permutation(nums: &mut Vec<i32>) {
        fn swap(nums: &mut Vec<i32>, i: usize, j: usize) {
            let temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
        }

        let mut i = nums.len() - 2;
        while i as i32 >= 0 && nums[i] >= nums[i + 1] {
            i -= 1;
        }
        if i as i32 >= 0 {
            let mut j = nums.len() - 1;
            while j as i32 >= 0 && nums[i] >= nums[j] {
                j -= 1;
            }
            swap(nums, i, j);
        }
        let (mut left, mut right) = (i + 1, nums.len() - 1);
        while left < right {
            swap(nums, left, right);
            left += 1;
            right -= 1;
        }
    }
}

go

func nextPermutation(nums []int)  {
    i := len(nums) - 2
	for i >= 0 && nums[i] >= nums[i+1] {
		i--
	}
	if i >= 0 {
		j := len(nums) - 1
		for j >= 0 && nums[i] >= nums[j] {
			j--
		}
		nums[i], nums[j] = nums[j], nums[i]
	}
	left, right := i+1, len(nums)-1
	for left < right {
		nums[left], nums[right] = nums[right], nums[left]
		left++
		right--
	}
}

c++

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int i = nums.size() - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            --i;
        }
        if (i >= 0) {
            int j = nums.size() - 1;
            while (j >= 0 && nums[i] >= nums[j]) {
                --j;
            }
            swap(nums[i], nums[j]);
        }
        reverse(nums.begin() + i + 1, nums.end());
    }
};

c

void swap(int *nums, int left, int right) {
    int temp = nums[left];
    nums[left] = nums[right];
    nums[right] = temp;
}

void nextPermutation(int *nums, int numsSize) {
    int i = numsSize - 2;
    while (i >= 0 && nums[i] >= nums[i + 1]) {
        --i;
    }
    if (i >= 0) {
        int j = numsSize - 1;
        while (j >= 0 && nums[i] >= nums[j]) {
            --j;
        }
        swap(nums, i, j);
    }
    int left = i + 1, right = numsSize - 1;
    while (left < right) {
        swap(nums, left, right);
        ++left;
        --right;
    }
}

python

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = len(nums) - 2
        while i >= 0 and nums[i] >= nums[i + 1]:
            i -= 1
        if i >= 0:
            j = len(nums) - 1
            while j >= 0 and nums[i] >= nums[j]:
                j -= 1
            nums[i], nums[j] = nums[j], nums[i]
        left, right = i + 1, len(nums) - 1
        while left < right:
            nums[left], nums[right] = nums[right], nums[left]
            left += 1
            right -= 1

java

class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            --i;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (j >= 0 && nums[i] >= nums[j]) {
                --j;
            }
            swap(nums, i, j);
        }
        int left = i + 1, right = nums.length - 1;
        while (left < right) {
            swap(nums, left, right);
            ++left;
            --right;
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}