卡方检验的基本原理详解
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 一、卡方检验基本原理
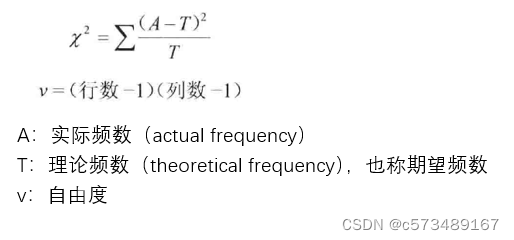
- 1. 1 χ2统计量计算公式
- 1.2 理论频数如何计算?
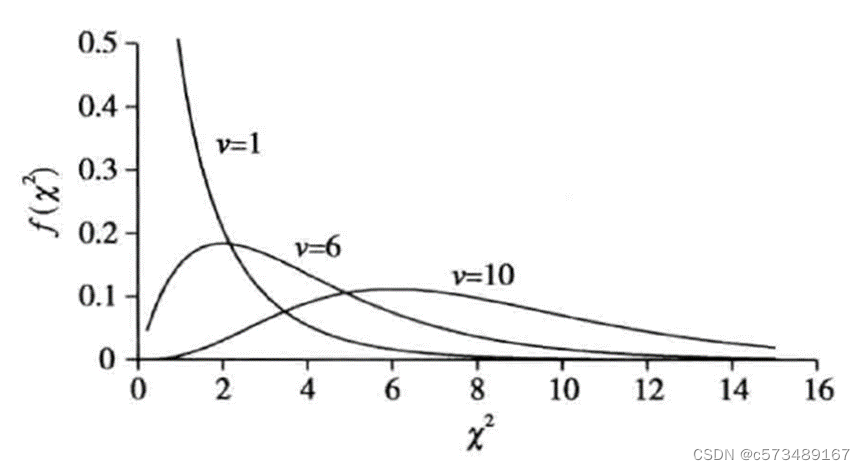
- 1.3 χ2值的结果如何理解?
- 1.4 χ2检验的自由度如何理解?
- 1.5 χ2检验的步骤
- 1.6 四格表专用公式
- 1.7 为什么在样本量较小或理论频数较小时,不能使用χ2检验?
- 二、配对χ2检验
- 2.1 什么是配对?
- 2.2 配对χ2的统计量
- 2.2 配对χ2检验的步骤
- 三、行*列资料的χ2检验
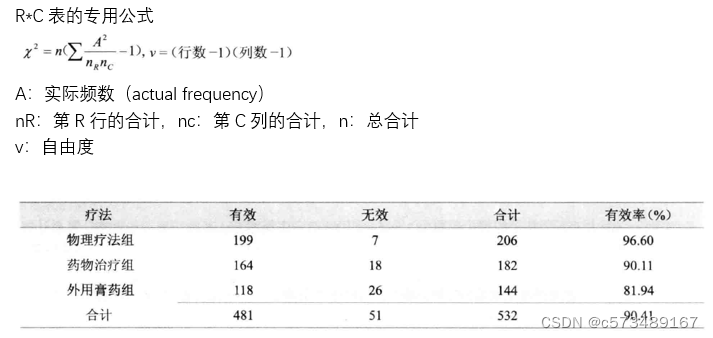
- 3.1 行*列资料的χ2检验统计量
- 3.2 行*列资料的χ2检验步骤
- 3.3 行*列资料的χ2检验的应用
- 3.4 R*C表χ2检验的注意事项
- 3.5 R*C表资料的检验方法选择
- 四、多样本率间的多重比较
- 五、CMH χ2统计量(Cochran-Mantel-Haenszel χ2检验)
- 5.1 CMH χ2统计量的分类
- 五、拟合优度检验
一、卡方检验基本原理
比较试验组和对照组的疗效(有效率),将200例患者1:1随机分配为两组,结果如下:

abcd的四个数组成了四格表(fourfold table),也称列联表(contingency table)。
比较试验组和对照组的有效率是否有差异?即试验组85.29%的有效率与对照组66.33%之间是否有统计学差异?(目的)
两样本率的比较,用chi-square检验两样本总体率是否有差异。(方法)
1. 1 χ2统计量计算公式
1.2 理论频数如何计算?
基于原假设H0:π1=π2确定。即试验组和对照组的有效率相等。
总体的有效率:(a+c)/(a+b+c+d) 152/200=76%
a理论频数:(a+b)76% 10276%=77.52
c理论频数:(c+d)76% 9876%=74.48
理论频数计算公式:

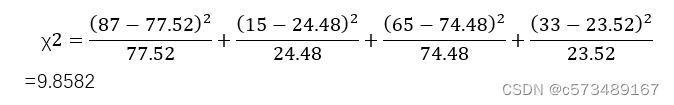
1.3 χ2值的结果如何理解?
1.4 χ2检验的自由度如何理解?
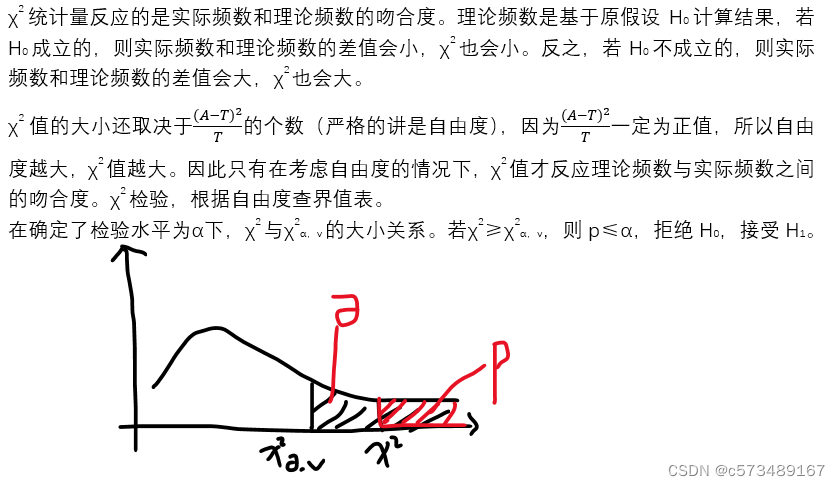
χ2检验的自由度v取决于自由取值的格子数,不是样本量。四格表只有两行两列,v=1。当周边合计固定的情况下,4个数只有一个可以自由取值。计算出一个理论频数后,其他3个可以通过周边合计计算出来。
1.5 χ2检验的步骤
Step1:建立假设
H0:π1=π2 即试验组与对照组有效率相等
H1:π1≠π2 即试验组与对照组有效率不相等
α=0.05
Step2:计算理论频数,统计量
χ2= 9.8582
Step3:根据自由度查χ2检验界值表,在α水平下,得出结论
p=0.0017 p<0.05
拒绝H0,接受H1,试验组和对照组有效率不相等。
1.6 四格表专用公式
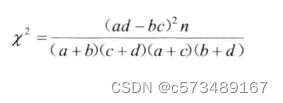

公式的使用方法
(1) n≥40,且所有的T≥5(理论频数)时,用χ2基本公式或四格表专用公式。P≈α,采用Fisher确切概率法。
(2) n≥40,且所有的1≤T≤5时,用校正公式,或用Fisher确切概率法。
(3) n<40,或T<1时,用Fisher确切概率法。
1.7 为什么在样本量较小或理论频数较小时,不能使用χ2检验?
χ2分布是一个连续的分布,只有一个参数,自由度。
计数资料的实际频数是分类资料,是不连续的,计算的χ2值是离散型分布。当样本量很小的时候,计算出的概率偏小。因此需要校正。
二、配对χ2检验
2.1 什么是配对?
对样本中各观察单位(每个患者)分别用两种方法处理,然后观察两种处理方法的某两分类变量的计数结果。处理包括:两种检验方法、培养方法、诊断方法等。
a:A方法和B方法均检验为阳性的例数
b:A方法阳性,B方法阴性的例数
c:A方法阴性,B方法阳性的例数
d:A方法和B方法均检验为阴性的例数
a和d为两种方法一致的情况,c和b为两种方法不一致的情况。
两种方法无差别时,b=c。

2.2 配对χ2的统计量
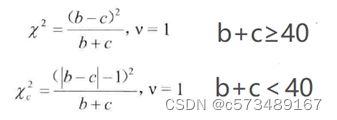
说明:当n很大且a和d的数值很大(两方法抑制率较高),b和c的数值相对较小,即便检验结果有统计学意义,其实际意义往往不大,该方法不适用。因为该方法仅考虑了两方法不一致的情况(b、c),未考虑样本含量n和两方法一致的情况(a、d)。
2.2 配对χ2检验的步骤
Step1:建立假设
H0:B=C 即两种方法检测结果相同
H1:B≠C 即两种方法检测结果不相同
α=0.05
Step2:计算理论频数,统计量
因b+c<40,所以采用校正公式。
χ2=(|12-2|-1)^2/(12+2) = 5.79
Step3:根据自由度查χ2检验界值表,在α水平下,得出结论
p<0.05,拒绝H0,接受H1,试验组和对照组有效率不相等。
三、行*列资料的χ2检验
3.1 行*列资料的χ2检验统计量
3.2 行*列资料的χ2检验步骤
Step1:建立假设
H0:π1=π2 =π3 即3种方法的有效率相等
H1:π1≠π2≠π3 即3种方法的有效率不全相等
α=0.05
Step2:计算统计量
χ2= 21.04 v=(3-1)*(2-1)=2
Step3:根据自由度查χ2检验界值表,在α水平下,得出结论
p<0.05
拒绝H0,接受H1,3种治疗方法有差别。
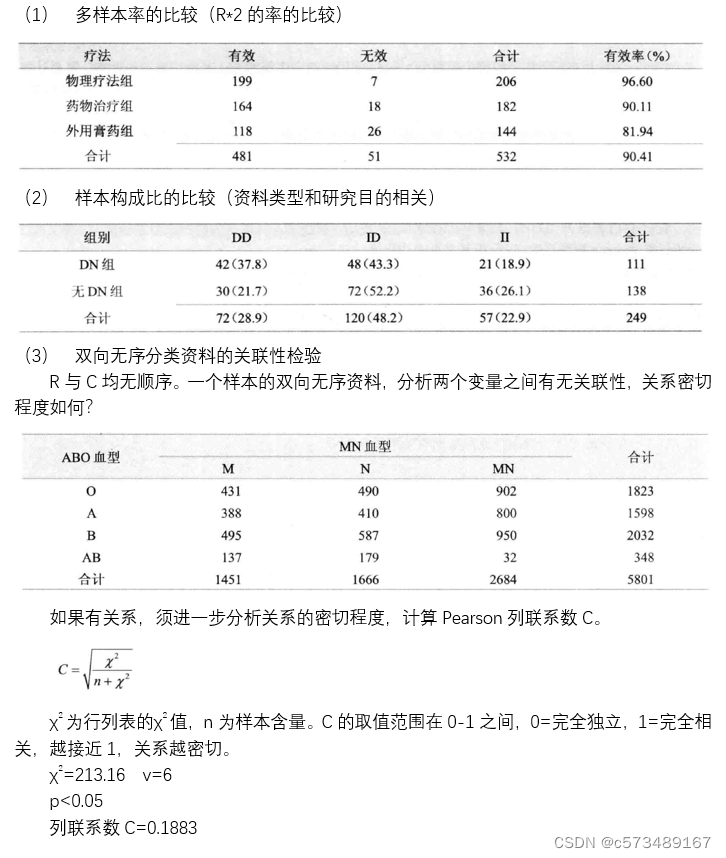
3.3 行*列资料的χ2检验的应用
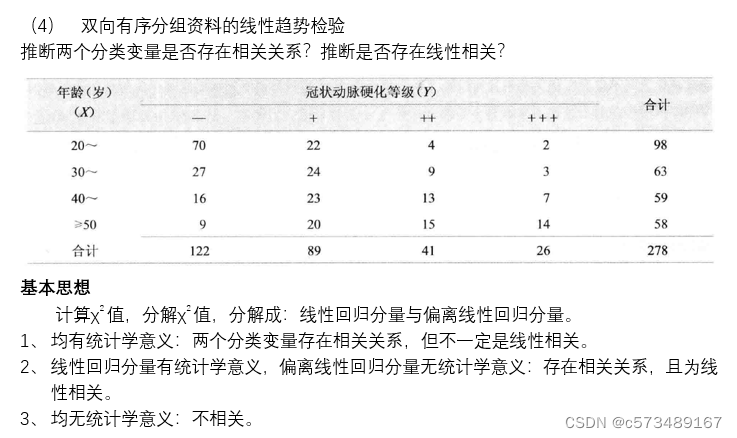

3.4 R*C表χ2检验的注意事项
(1) 行列表中理论频数太小(T<1,1≤T≤5的格子数超过1/5),解决方法:
1、 增加样本量,扩大理论频数;
2、 根据专业知识合并或删除
3、 双向无序R*C表的Fisher确切概率法。
(2) 多样本率的比较,拒绝H0,仅认为各总体率之间总的来说是有差异的,不能说明任一两个样本之间存在差异。
(3) 有序分类资料不宜用χ2检验,因为行列表的χ2检验与分类变量的顺序无关,行列的频数互换,所得的χ2值是不变的,但对于有序分类变量这是不妥的。根据分类类型和研究目的选择恰当的检验方法(秩和检验)。
3.5 R*C表资料的检验方法选择
(1) 双向无序:多样本率、构成比的比较,两分类变量之间的关联性(独立性)检验。
(2) 单向有序(看指标变量是否是有序的)
1、 R有序,C无序:分组变量(年龄)有序,指标变量(疾病种类)无序,研究分析不同年龄组各疾病的构成情况,采用χ2检验。
2、 R无序,C有序:分组变量(治疗方法)无序,指标变量(严重程度)有序,比较不同治疗方法的疗效,采用秩和检验。
(3) 双向有序(属性相同):四格表配对资料的扩展,两种方法同时对一批样本的测定结果。研究目的是分析两种检测方法的一致性,采用一致性检验或Kappa检验。
(4) 双向有序(属性不同)
1、 分析目的与分组的序列无关,将其视为单项有序R*C资料。不同年龄组患者之间疗效是否有差异。采用秩和检验。
2、 分析两个有序分类变量之间是否存在相关关系,采用等级相关分析。
3、 分析两个有序分类变量之间是否存在线性变化趋势,采用线性趋势检验。
四、多样本率间的多重比较
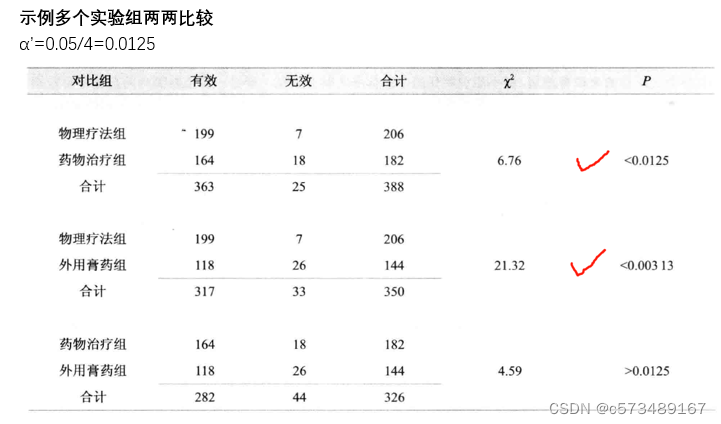
多样本率的比较的R*C表χ2检验,拒绝H0,接受H1时,只能认为总体率有差别,不能认为任一两两有差异。进一步推断具体哪两个有差异,不能直接进行两两χ2检验,会增加I类错误。采用χ2分割法,Scheffe’可信区间法,SNK法。
χ2分割法基本原理
重新规定检验水准,目的是控制I类错误,保证α不变。
α^'=α/比较次数
(1)多个实验组两两比较
比较次数=(k(k-1))/2+1 k=组别数
(2)多个实验组与同一个对照组比较
比较次数=2(k-1) k=组别数
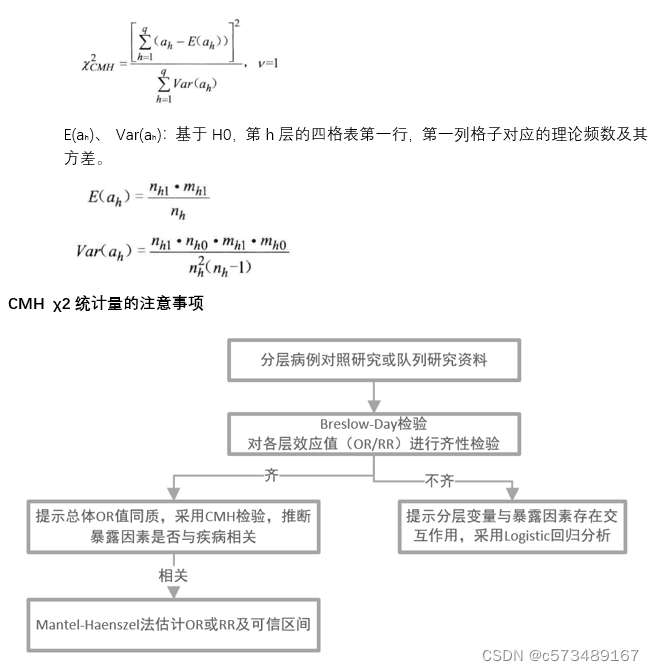
五、CMH χ2统计量(Cochran-Mantel-Haenszel χ2检验)
高维列联表的分析,控制了某一个或几个混杂因素(分层变量)之后,检验二维R*C表中行变量X与列变量Y之间是否存在统计学关联。
H0:任一层的行变量与列变量均不相关
H1:至少存在一层行变量与列变量均相关
当各层行变量与列变量相关的方向不一致时,CMH统计量的检验效能较低。
5.1 CMH χ2统计量的分类
(1) 相关统计量
X、Y均为有序变量,自由度为1。
(2) 方差分析统计量(行平均得分统计量)
Y为有序变量,自由度为R-1。
H0:所有层的各行Y变量平均得分均相等
H1:至少又一层各行Y变量平均得分均不相等
一维R*C列联表=各行Y变量平均得分的方差分析
秩和检验:Kruskal-Wallis检验。
(3) 一般关联统计量
X、Y均为无序分类资料,目的是检验是否有关联性。
分层变量校正的Pearson χ2统计量。自由度(R-1)*(C-1)。
CMH χ2统计量(以四格表为例)
第h层的四格表

五、拟合优度检验
推断频率分布是否符合某一理论分布。
