当前位置： 首页 > news >正文

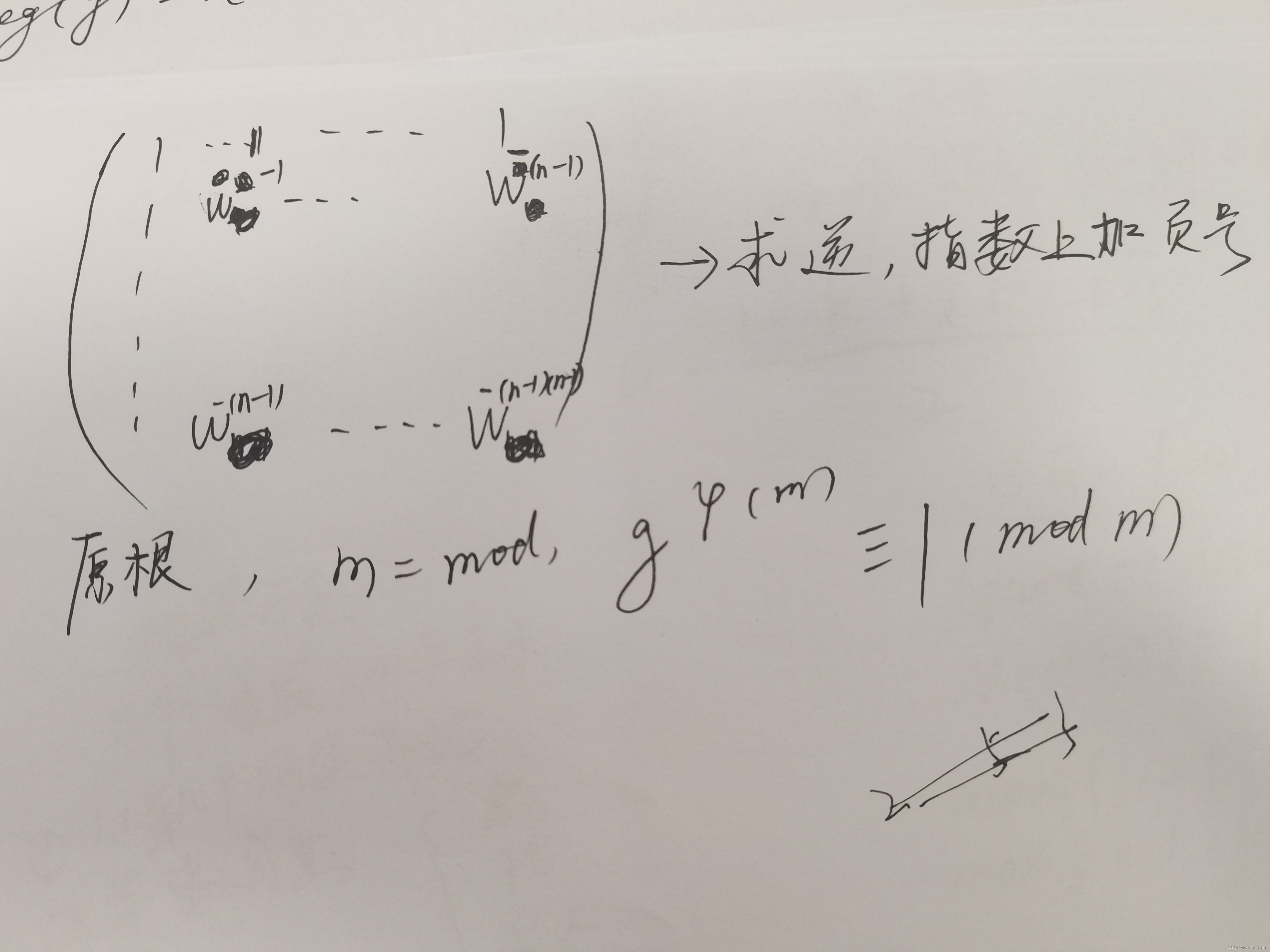
FFT 快速傅里叶变换 NTT 快速数论变换

news 来源：原创 2024/12/21 11:09:32

SDNU 1531 a*b III (FFT模板)

Description
计算a乘b，多组输入（50组以内）。
Input
输入a b，数据范围0 <= a,b <= 10^100000。
Output
输出a与b的乘积。
Sample Input
2 2
4 4
Sample Output
4
16
Hint
FFT

FFT的原理是。。。（乱记的），大概原理懂了

在这里插入图片描述
在这里插入图片描述

AC代码：

#include<bits/stdc++.h>

using namespace std;

const double PI = acos(-1.0);
struct Complex
{
    double x,y;
    Complex(double _x = 0.0,double _y = 0.0)
    {
        x = _x;
        y = _y;
    }
    Complex operator -(const Complex &b)const
    {
        return Complex(x-b.x,y-b.y);
    }
    Complex operator +(const Complex &b)const
    {
        return Complex(x+b.x,y+b.y);
    }
    Complex operator *(const Complex &b)const
    {
        return Complex(x*b.x-y*b.y,x*b.y+y*b.x);
    }
};

void change(Complex y[],int len)
{
    int i,j,k;
    for(i = 1, j = len/2; i <len-1; i++)
    {
        if(i < j)
            swap(y[i],y[j]);
        k = len/2;
        while(j >= k)
        {
            j -= k;
            k /= 2;
        }
        if(j < k)
            j += k;
    }
}

void fft(Complex y[],int len,int on)
{
    change(y,len);
    for(int h = 2; h <= len; h <<= 1)
    {
        Complex wn(cos(-on*2*PI/h), sin(-on*2*PI/h));
        for(int j = 0; j < len; j+=h)
        {
            Complex w(1,0);
            for(int k = j; k < j+h/2; k++)
            {
                Complex u = y[k];
                Complex t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1)
        for(int i = 0; i < len; i++)
            y[i].x /= len;
}

const int MAXN = 200010;
Complex x1[MAXN],x2[MAXN];
char str1[MAXN/2],str2[MAXN/2];
int sum[MAXN];

int main()
{
    while(~scanf("%s%s",str1,str2))
    {
        int len1 = strlen(str1);
        int len2 = strlen(str2);
        int len = 1;
        while(len < len1*2 || len < len2*2) len<<=1;

        for(int i = 0; i < len1; i++) x1[i] = Complex(str1[len1-1-i]-'0',0);

        for(int i = len1; i < len; i++) x1[i] = Complex(0,0);

        for(int i = 0; i < len2; i++) x2[i] = Complex(str2[len2-1-i]-'0',0);

        for(int i = len2; i < len; i++) x2[i] = Complex(0,0);

        fft(x1,len,1);
        fft(x2,len,1);

        for(int i = 0; i < len; i++) x1[i] = x1[i]*x2[i];

        fft(x1,len,-1);
        for(int i = 0; i < len; i++) sum[i] = (int)(x1[i].x+0.5);

        for(int i = 0; i < len; i++)
        {
            sum[i+1]+=sum[i]/10;
            sum[i]%=10;
        }
        len = len1+len2-1;

        while(sum[len] <= 0 && len > 0) len--;

        for(int i = len; i >= 0; i--) printf("%c",sum[i]+'0');

        printf("\n");
    }
    return 0;
}

SDNU 1532 a*b IV（NTT模板）

Description
计算a*b，多组输入（50组以内）。
Input
两个数a,b,数据范围 0<=a,b<=10^100000。
Output
输出a与b的乘积。
Sample Input
2 2
4 4
Sample Output
4
16
Hint
NTT

AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

//拓展欧几里得
void exgcd(ll a, ll b, ll &x, ll &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return;
    }
    ll x0, y0;
    exgcd(b, a % b, x0, y0);
    x = y0;
    y = x0 - (ll)(a / b) * y0;
}

//求逆元
ll Inv(ll a, ll p)
{
    ll x, y;
    exgcd(a, p, x, y);
    x %= p;
    while (x < 0) x += p;
    return x;
}

//快速幂取模
ll qpow(ll a, ll b, ll p)
{
    if (b < 0)
    {
        b = -b;
        a = Inv(a, p);
    }
    ll ans = 1, mul = a % p;
    while (b)
    {
        if (b & 1) ans = ans * mul % p;
        mul = mul * mul % p;
        b >>= 1;
    }
    return ans;
}

//在模p意义下的计算
#define maxn (65537*2)
const int MOD = 479 * (1 << 21) + 1, G = 3;
//const ll MOD = 15 * (1 << 27) + 1, G = 31;

//翻转数组
ll rev[maxn];

void get_rev(ll bit)
{
    for (ll i = 0; i < (1 << bit); i++)
    {
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
    }
}

//存储数组
ll ar[maxn], br[maxn];

//快速数论变换
void ntt(ll *a, ll n, ll dft)
{
    //翻转
    for (ll i = 0; i < n; i++)
    {
        if (i < rev[i]) swap(a[i], a[rev[i]]);
    }
    //蝴蝶操作模拟
    for (ll step = 1; step < n; step <<= 1)
    {
        ll wn;
        wn = qpow(G, dft * (MOD - 1) / (step * 2), MOD);
        for (ll j = 0; j < n; j += (step << 1))
        {
            ll wnk = 1;//这里一定要用long long不然会迷之溢出
            for (ll k = j; k < j + step; k++)
            {
                ll x = a[k] % MOD, y = (wnk * a[k + step]) % MOD;//这里也要用long long
                a[k] = (x + y) % MOD;
                a[k + step] = ((x - y) % MOD + MOD) % MOD;
                wnk = (wnk * wn) % MOD;
            }
        }
    }
    if (dft == -1)
    {
        ll nI = Inv(n, MOD);
        for (ll i = 0; i < n; i++) a[i] = a[i] * nI % MOD;
    }
}

//输入数组
char s1[maxn], s2[maxn];

int main()
{
    while (~scanf("%s%s", s1, s2)) {
        ll l1 = strlen(s1), l2 = strlen(s2);
        for (ll i = 0; i < l1; i++) ar[i] = s1[l1 - i - 1] - '0';
        for (ll i = 0; i < l2; i++) br[i] = s2[l2 - i - 1] - '0';

        ll bit, s = 2;
        for (bit = 1; (1 << bit) < (l1 + l2 - 1); bit++) s <<= 1;

        get_rev(bit);
        ntt(ar, s, 1);
        ntt(br, s, 1);

        for (ll i = 0; i < s; i++) ar[i] = ar[i] * br[i] % MOD;

        ntt(ar, s, -1);
        for (ll i = 0; i < s; i++)
        {
            ar[i + 1] += ar[i] / 10;
            ar[i] %= 10;
        }
        ll cnt = s;

        while (cnt >= 0 && ar[cnt] == 0) cnt--;

        for (ll i = cnt; i >= 0; i--) printf("%lld", ar[i]);

        if (cnt == -1) putchar('0');

        putchar('\n');

        memset(ar, 0, sizeof(ar));
        memset(br, 0, sizeof(br));
    }
    return 0;
}

21牛客暑假多校训练营第一场H题Hash Function

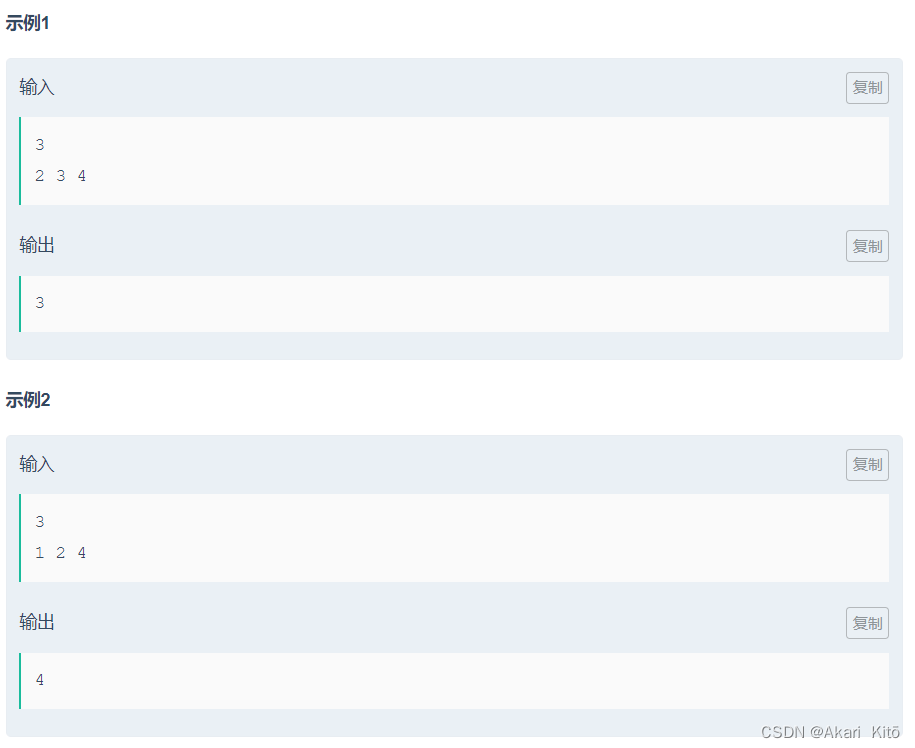
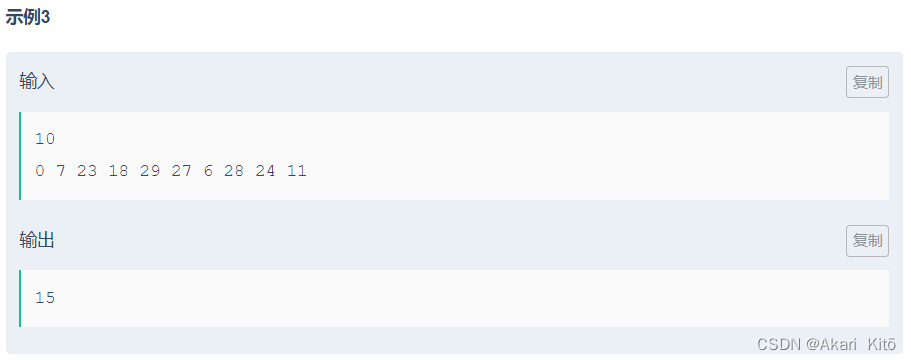
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
题意：
输入n，之后n个数，找最小的一个正整数p满足这n个数模p取得数字都不相同。
分析：
对于任意1<=i，j<=n&&i!=j满足ai%p!=aj%p,即|ai-aj|%p != 0,一旦有了任意两个数的差值，之后暴力枚举p即可。
暴力求任意两个数的差值是O(n^2),比较快的方法是转化为多项式乘法，构造两个多项式 ∑ 1 n x a i \sum_{1}^{n}{x^{a_i}} ∑1n​xai​和 ∑ 1 n x − a i \sum_{1}^{n}{x^{-a_i}} ∑1n​x−ai​,让两个多项式相乘，得到多项式 ∑ x b i \sum{x^{b_i}} ∑xbi​, ∣ b i ∣ |b_i| ∣bi​∣的所有取值就是任意两个数字的差值（0除外，因为保证了 a i ! = b i a_i!=b_i ai​!=bi​）。多项式相乘的过程可以通过FFT或者NTT实现，由于数组下标无法是0，所以第二个多项式可以构造为 ∑ 1 n x M X − a i \sum_{1}^{n}{x^{MX-a_i}} ∑1n​xMX−ai​即将指数加上一个偏移量MX，偏移量MX应该设置为一个稍大于5e5的数据（不懂原因，我觉得ai最大值为5e5，MX设置为5e5即可，但是这样确实被一个样例卡了，duipai了很久也没找出来）。
之后暴力枚举每个数字p，判断p的倍数是否出现即可，这个过程是 O ( n l o n g n ) O(nlongn) O(nlongn)的。
AC代码：
FFT

#include<bits/stdc++.h>

using namespace std;

const double PI = acos(-1.0);
struct Complex
{
    double x,y;
    Complex(double _x = 0.0,double _y = 0.0)
    {
        x = _x;
        y = _y;
    }
    Complex operator -(const Complex &b)const
    {
        return Complex(x-b.x,y-b.y);
    }
    Complex operator +(const Complex &b)const
    {
        return Complex(x+b.x,y+b.y);
    }
    Complex operator *(const Complex &b)const
    {
        return Complex(x*b.x-y*b.y,x*b.y+y*b.x);
    }
};

void change(Complex y[],int len)
{
    int i,j,k;
    for(i = 1, j = len/2; i <len-1; i++)
    {
        if(i < j)
            swap(y[i],y[j]);
        k = len/2;
        while(j >= k)
        {
            j -= k;
            k /= 2;
        }
        if(j < k)
            j += k;
    }
}

void fft(Complex y[],int len,int on)
{
    change(y,len);
    for(int h = 2; h <= len; h <<= 1)
    {
        Complex wn(cos(-on*2*PI/h), sin(-on*2*PI/h));
        for(int j = 0; j < len; j+=h)
        {
            Complex w(1,0);
            for(int k = j; k < j+h/2; k++)
            {
                Complex u = y[k];
                Complex t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1)
        for(int i = 0; i < len; i++)
            y[i].x /= len;
}

const int MAXN = 1050010;
const int MX = 500005;
Complex x1[MAXN],x2[MAXN];
int n;
int ar[MAXN>>1];
int sum[MAXN];
int len1, len2;
bool boo1[MAXN>>1], boo2[MAXN>>1];
bool vis[MAXN>>1];
bool flag;

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
    {
        scanf("%d", &ar[i]);
        boo1[ar[i]] = true;
        boo2[MX-ar[i]] = true;
    }

    if(n == 1) 
    {
        printf("1\n");
        return 0;
    }
    
    len1 = len2 = MX;
    int len = 1;
    while(len < len1*2 || len < len2*2) len<<=1;

    for(int i = 1; i <= n; ++i) x1[ar[i]] = Complex(1, 0);
    for(int i = 1; i <= n; ++i) x2[MX-ar[i]] = Complex(1, 0);

    for(int i = 0; i < len; i++)
    {
        if(!boo1[i]) x1[i] = Complex(0, 0);
        if(!boo2[i]) x2[i] = Complex(0, 0);
    }

    fft(x1,len,1);
    fft(x2,len,1);

    for(int i = 0; i < len; i++) x1[i] = x1[i]*x2[i];

    fft(x1,len,-1);
    for(int i = 0; i < len; i++) sum[i] = (int)(x1[i].x+0.5);

    for(int i = 1; i <= MX; ++i) if(sum[i+MX] != 0) vis[i] = true;

    for(int i = 1; i <= MX; ++i)
    {
        flag = false;
        for(int j = i; j <= MX; j += i)
        {
            if(vis[j])
            {
                flag = true;
                break;
            }
        }
        if(!flag)
        {
            printf("%d\n", i);
            break;
        }
    }

    return 0;
}

NTT

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

//拓展欧几里得
void exgcd(ll a, ll b, ll &x, ll &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return;
    }
    ll x0, y0;
    exgcd(b, a % b, x0, y0);
    x = y0;
    y = x0 - (ll)(a / b) * y0;
}

//求逆元
ll Inv(ll a, ll p)
{
    ll x, y;
    exgcd(a, p, x, y);
    x %= p;
    while (x < 0) x += p;
    return x;
}

//快速幂取模
ll qpow(ll a, ll b, ll p)
{
    if (b < 0)
    {
        b = -b;
        a = Inv(a, p);
    }
    ll ans = 1, mul = a % p;
    while (b)
    {
        if (b & 1) ans = ans * mul % p;
        mul = mul * mul % p;
        b >>= 1;
    }
    return ans;
}

//在模p意义下的计算
#define maxn (2000005)
const int MOD = 479 * (1 << 21) + 1, G = 3;
//const ll MOD = 15 * (1 << 27) + 1, G = 31;

//翻转数组
ll rev[maxn];

void get_rev(ll bit)
{
    for (ll i = 0; i < (1 << bit); i++)
    {
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
    }
}

//存储数组
ll ar[maxn], br[maxn];

//快速数论变换
void ntt(ll *a, ll n, ll dft)
{
    //翻转
    for (ll i = 0; i < n; i++)
    {
        if (i < rev[i]) swap(a[i], a[rev[i]]);
    }
    //蝴蝶操作模拟
    for (ll step = 1; step < n; step <<= 1)
    {
        ll wn;
        wn = qpow(G, dft * (MOD - 1) / (step * 2), MOD);
        for (ll j = 0; j < n; j += (step << 1))
        {
            ll wnk = 1;//这里一定要用long long不然会迷之溢出
            for (ll k = j; k < j + step; k++)
            {
                ll x = a[k] % MOD, y = (wnk * a[k + step]) % MOD;//这里也要用long long
                a[k] = (x + y) % MOD;
                a[k + step] = ((x - y) % MOD + MOD) % MOD;
                wnk = (wnk * wn) % MOD;
            }
        }
    }
    if (dft == -1)
    {
        ll nI = Inv(n, MOD);
        for (ll i = 0; i < n; i++) a[i] = a[i] * nI % MOD;
    }
}

//输入数组
const int MX = 500005;
char s1[maxn], s2[maxn];
int n;
int arr[maxn];
bool boo1[MX + 5], boo2[MX + 5];
bool vis[MX + 5];
bool flag;

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
    {
        scanf("%d", &arr[i]);
        boo1[arr[i]] = true;
        boo2[MX-arr[i]] = true;
    }

    ll l1 = MX + 1, l2 = MX + 1;
    for(int i = 1; i <= n; ++i)
    {
        ar[arr[i]] = 1;
        br[MX-arr[i]] = 1;
    }

    ll bit, s = 2;
    for (bit = 1; (1 << bit) < (l1 + l2 - 1); bit++) s <<= 1;

    get_rev(bit);
    ntt(ar, s, 1);
    ntt(br, s, 1);

    for (ll i = 0; i < s; i++) ar[i] = ar[i] * br[i] % MOD;

    ntt(ar, s, -1);

    for(int i = 1; i <= MX; ++i) if(ar[i+MX] != 0) vis[i] = true;

    for(int i = 1; i <= MX; ++i)
    {
        flag = false;
        for(int j = i; j <= MX; j += i)
        {
            if(vis[j])
            {
                flag = true;
                break;
            }
        }
        if(!flag)
        {
            printf("%d\n", i);
            break;
        }
    }

    return 0;
}

相关文章：

  • 政府网站建设工作情况汇报/app拉新接单平台
  • 网站设计与建设论文开题报告/我国网络营销现状分析
  • 一学一做短视频网站/百度网盘下载官网
  • 网站开发工具与技术/太原网络推广公司
  • 做防护信息的网站/广告营销策划方案模板
  • 上海网站建设q479185700棒/樱花12e56
  • 王传福赚嗨了！比亚迪单季利润超50亿 还大量出口到欧洲
  • 带你趣学算法
  • 设计模式（四）—— 装饰者模式
  • [架构之路-48]：目标系统 - 系统软件 - Linux下的网络通信-4-快速数据平面开发套件DPDK-工作原理
  • 创意电子学00课：需要准备的材料汇总
  • 什么是轨到轨？这种运放和普通运放比有什么特点和优点？
  • 面试官：小伙子，说说C/C++是如何进行内存管理的？我：……
  • STL容器 —— map和set的模拟实现
  • 软考知识点---06文件管理与作业管理---01文件管理
  • API网关基础认知
  • 腾讯云Ubuntu18.04配置深度学习环境
  • 反常积分敛散性的比较判别法专题（及常用反常积分）