洛谷千题详解 | P1010 [NOIP1998 普及组] 幂次方【C++、Java、Python、Pascal语言】
博主主页:Yu·仙笙
专栏地址:洛谷千题详解
目录
题目描述
输入格式
输出格式
输入输出样例
解析:
C++源码:
Pascal源码:
Java源码:
Python源码:
-------------------------------------------------------------------------------------------------------------------------------
 -------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------
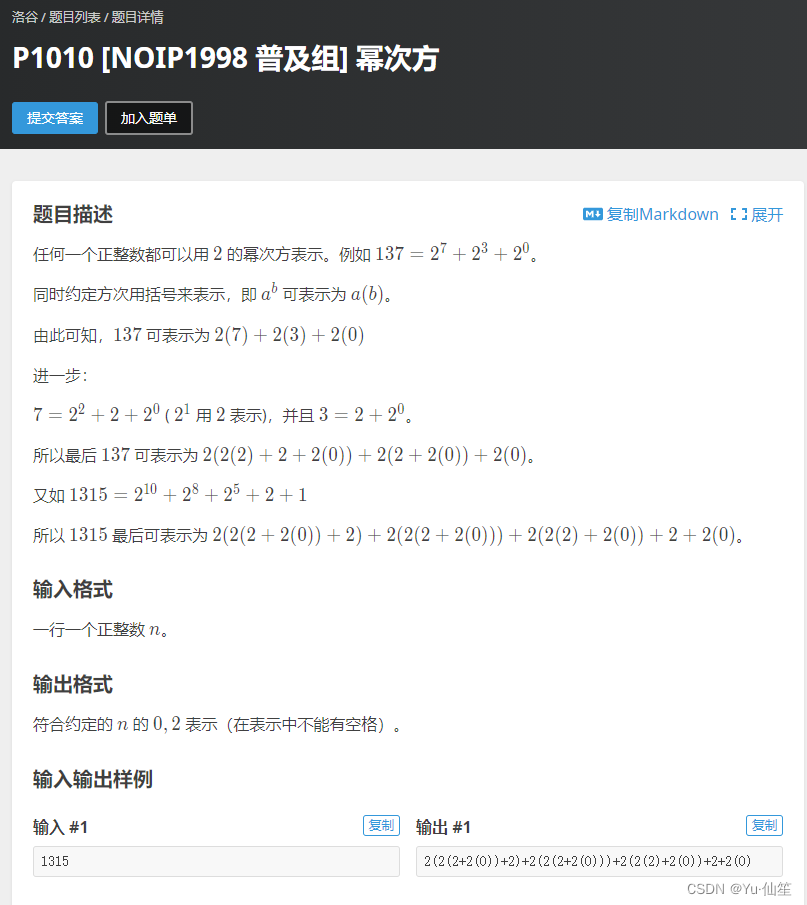
题目描述
任何一个正整数都可以用 2 的幂次方表示。例如 137=27+23+20。
同时约定方次用括号来表示,即 a^b 可表示为 a(b)。
由此可知,137可表示为 2(7)+2(3)+2(0)
进一步:
7= 2^2+2+2^0 ( 2^1 用 2 表示),并且 3=2+2^0
所以最后 137可表示为 2(2(2)+2+2(0))+2(2+2(0))+2(0)。
又如 1315=2^10+2^8 +2^5 +2+1
所以 1315 最后可表示为 2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)。
-------------------------------------------------------------------------------------------------------------------------------
输入格式
一行一个正整数 n。
-------------------------------------------------------------------------------------------------------------------------------
输出格式
符合约定的 n 的 0,2 表示(在表示中不能有空格)。
-------------------------------------------------------------------------------------------------------------------------------
输入输出样例
输入#1
1315
输出 #1
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
-------------------------------------------------------------------------------------------------------------------------------
解析:
我们知道,二进制数表示的其实就是一个正整数分解成为2的幂次方和!
如3用二进制表示为 11 ,从右到左分别是第0位,第1位……
则3=2^1+2^0(只要二进制那位是一,就是2^(这一位))
再比如10 二进制是1010,则10=2^3+2^1;
大家自己体会一下
下面更高级的:位运算(其实也不高级,就是没人做)
不会位运算的就用上面那种吧,个人觉得位运算更快(普通14ms,位运算11ms)
位运算具体问度娘吧
思路如下:
遍历n的二进制(从地位到高位),用数组储存该位为1的位数;如1010(即10),先记录第1位是1,最后记录到第3位是1;
遍历完成后,对高位先进行处理(即原来为i++,现在变为i--)
该位(就是幂的次数)大于2,,递归再次处理
一旦处理到该位小于3,输出;
-------------------------------------------------------------------------------------------------------------------------------
C++源码:
#include<cstdio>
using namespace std;
void ASCII(int m)
{
int i=0,k=m,u=0,h[50];
while(k)//位运算实现;
{
if(k&1)h[++u]=i;
//h[++u]相当于++u,h[u]……
k>>=1;
i++;
}
//据上面写的,u从1开始,无论如何一定会有输出;
while(u)//u为真
{
if(h[u]<3)//具体括号判断;
{
if(h[u]==1 && u-1!=0) printf("2+");
else if(h[u]==1) printf("2");
if((h[u]==0||h[u]==2)&&(u-1!=0)) printf("2(%d)+",h[u]);
else if(h[u]==0||h[u]==2) printf("2(%d)",h[u]);
--u;//搜索下一个;
}
else
{
printf("2(");
ASCII(h[u--]);
//相当于h[u],--u;
//这里千万不能写成 h[--u],否则你会3个WA两个MLE;
if(u!=0)printf(")+");
//由于u进行了自减,此时的u已经是下一个数了;
else printf(")");
//判断括号;
}
}
}
int main()
{
int n;
scanf("%d",&n);
ASCII(n);
return 0;//别忘了写;
}-------------------------------------------------------------------------------------------------------------------------------
Pascal源码:
type num=array[0..100000] of longint;
var i,j,k,l,n,m,o,p,h:longint;
//这里的a[0]指数组长度。
function ejz(s:longint):num;//要转的数
var i,j,k:longint;
ans:num;
begin
i:=s; j:=0; k:=0; //让变量i赋值为要转的数s
fillchar(ejz,sizeof(ejz),0);
fillchar(ans,sizeof(ans),0);
while i>0 do
begin
inc(j);
ejz[j]:=i mod 2;
i:=i div 2; //转2进制的过程在此。
end;
for i:=j downto 1 do
if ejz[i]=1 then begin inc(k); ans[k]:=i-1; end;//若2进制的第n位为1,那么数组中必有n-1。这个应该知道吧
ans[0]:=k;
exit(ans);
end;
procedure search(a:longint);
var n:num; i:longint;
begin
if a=0 then begin write('2(0)'); exit; end; //如果要处理0,那么...
if a=1 then begin write('2'); exit; end; //如果要处理1,那么...
n:=ejz(a);
for i:=1 to n[0]-1 do
begin
if (n[i]<>1) and (n[i]<>0) then write('2(');//这里要注意了!2^1不是2(1)!!!
search(n[i]);//递归处理数组里的数
if (n[i]<>1) and (n[i]<>0) then write(')');
write('+');//不要把加号输多了!
end;
if (n[n[0]]<>1) and (n[n[0]]<>0) then write('2(');
search(n[n[0]]);
if (n[n[0]]<>1) and (n[n[0]]<>0) then write(')');
end;
begin
readln(n);
search(n);
end.-------------------------------------------------------------------------------------------------------------------------------
Java源码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int a=sc.nextInt();
pow(a);
}
public static void pow(int a){
if(a>3){
int s=0;
int b=2;
while(b<=a){
b=b*2;
s++;
}
a=a-b/2;
System.out.print("2(");
pow(s);
if(s==3){
System.out.print("2+2(0)");
}
if(s==1){
System.out.print("2(0)");
}
if(s==2){
System.out.print("2");
}
System.out.print(")");
if(a==3){
System.out.print("+2+2(0)");
}
if(a==1){
System.out.print("+2(0)");
}
if(a==2){
System.out.print("+2");
}
if(a>3){
System.out.print("+");}
pow(a);
}
}
}
-------------------------------------------------------------------------------------------------------------------------------
Python源码:
def f1(x):
##获取一个数的幂
str0 = bin(int(str(x), 10))
str1 = str0[2:]
list1 = []
index = 0
for i in str1[::-1]:
if i == '1':
list1.append(index)
index += 1
list1.reverse()
return list1
def f2(list):
##格式化输出
list1 = [str(i) for i in list]
str2 = ''
for i in range(len(list1)):
if i < len(list1) - 1:
if list1[i] == "1":
str2 += "2+"
else:
if list[i] != 0:
str2 += "2({})+".format(f2(f1(list[i])))
else:
str2 += "2(0)"
if i == len(list1) - 1:
if list1[i] == "1":
str2 += "2"
else:
if list[i] != 0:
str2 += "2({})".format(f2(f1(list[i])))
else:
str2 += "2(0)"
return str2
n=int(input())
print(f2(f1(n)))
-------------------------------------------------------------------------------------------------------------------------------
