408 | 数据结构代码算法题模板技巧 之 单链表
若有错误,请指出!
一、数据结构定义
1.1 单链表结点结构体
typedef struct Lnode{
Elemtype data;
struct Lnode *next; //指向下一个结点的指针
}Lnode,*Linklist;1.2 双链表结点结构体
typedef struct LNode{
struct Lnode *prior,*next;
elemtype data;
}LNode,*Linklist;二、单链表的基本操作
2.1 头插法(插入到链表头)
注意具体使用时,p的后继丢失。需要保存。
viod HeadInsert(Linklist &L,int key){
Linklist p = new LNode;
p->data = key;
p->next = L->next; //重点
L->next = p; //重点
}2.2 尾插法(插入到链表尾)
void TailInsert(LinkList &L,int key){
Linklist p = new LNode;
p->data = key;
p->next = NULL;
Linklist q = L;
while(!q->next)
q = q->next;
q->next = p;
}
2.3 删除操作代码
void DeleteNode(Linklist &L,int &key){
Linklist p,q;
p = GetElem(L,i-1); //p指向删除位置的前驱结点
q = p->next;
key = q->data;
q->next = p->next;
free(q);
}2.2 逆置操作代码
void Rerverse(Linklist &L){
Linklist p = L->next , q = NULL;
L->next = NULL; //断链
while(!p){
q = p->next; //q指向p的后继
p->next = L->next; //头插法
L->next = p;
p = q;
}
}
2.3 前后指针代码
2.4 快慢指针代码 —— 获取链表中间结点、检测链表是否有环
最简单的方法是,先遍历一遍链表,计算出链表的长度,然后计算出中间节点的位置,然后再遍历一遍,边遍历边计算,直到找到中间节点,这个方法略显啰嗦,最坏的情况需要遍历2次链表,代码如下:

另一个更灵巧的方法是,用两个指针,慢指针每次走一步,快指针每次走两步,当快指针走到链表的末端(NULL)时,慢指针正好指向了中间节点,代码如下:
Linklist get_mid(Linklist L){
if(!L) return NULL;
Linklist slow = L;
Linklist fast = L->next;
while(fast && fast->next){
fast = fast->next->next;
slow = slow->next;
//fast走到末尾时,slow刚好在中间位置
return slow;
}三、习题练习
3.1 删除值为x的结点
viod Delete_x(Linklist &L,int x){
//L为带头结点的单链表,本算法删除L中所有值为x的结点
Linklist p = L->next, pre = L, q ; //q用于指向删除结点
while(p != NULL){
if(p->data == x){
q = p;
pre->next = p->next;
free(q);
p = p->next;
}
else{
pre = pre->next;
p = p->next;
}
}3.2 单链表就地逆置
试编写算法将带头结点的单链表就地逆置,所谓“就地”是指辅助空间复杂度为O(1)。
Linklist Reverse(Linklist L){
Linklist p = L->next,r; //p工作指针,遍历链表,r为p的后继,防止断链
L->next = NULL;
while(p != NULL){
r = p; //暂存p的后继
r->next = L->next; //头插法
L->next = r; //头插法
p = r;
}
return L; //若使用引用,则不必返回,且函数用void
}3.3 将链表排序
有一个带头结点的单链表L,设计一个算法使其元素递增有序。
void sort(Linklist &L){
//类似插入排序,先构造一个仅含一个结点的有序单链表
//再依次扫描原单链表剩下的结点,通过比较查找插入结点的前趋,插入有序单链表
Linklist p=L->next,pre;
Linklist r = p->next; //r保存p后继,防止断链
p->next = NULL; //构造一个仅含有一个结点的单链表
p = r; //从第三个结点开始
while(p){
r = p->next;
pre = L; //每次都从有序单链表头开始查找
while(p->data > pre->next->data && pre->next!=NULL)
//这里直接使用pre->next的值进行查找
//否则需要单独寻找插入结点前趋
pre = pre->next;
p->next = pre->next;
pre->next = p;
p = r;
}
}3.4 拆分链表
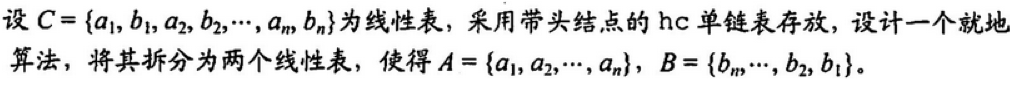

Linklist discreate(Linklist &A){
Linklist B = new LNode; //创建B表表头
B->next =NULL; //B表初始化
Linklist p = A->next; //p为工作指针
Linklist ra = A; //ra始终指向A的尾结点
while(p){
ra->next = p;
ra = ra->next; //p链到A表尾
p = p->next;
if(p){
p->next = q; //B表使用头插法,头插后p将断链
p->next = B->next;
B->next = p;
p = q;
}
}
ra->next = NULL;
return B;
}3.5 删除链表中的重复元素
在一个递增有序的线性表中,有数值相同的元素存在。
若存储方式为单链表,设计算法去掉数值相同的元素,使表中不再有重复的元素。
例如 (7,10,10,21,30,42,42,42,51,70) 将变为(7,10,21,30,42,51,70)。
void Deletesame(Linklist &L){
Linklist p = L->next,q;
if(p == NULL) return;
while(p->next){
q = p->next;
if(p->data == q->data){
p->next = q->next;
free(q);
}
else
p = p->next;
}
}3.6 将两个递增链表合并成一个递增链表
假设有两个按元素值递增次序排列的线性表,均以单链表形式存储。请编写算法将这两个单链表归并为一个按元素值递增次序排列的单链表,并要求利用原来两个单链表的结点存放归并后的单链表。
Linklist merge(Linklist L1,Linklist L2){
//合并两个递增有序单链表(带头结点),合并后链表递增排列
Linklist ra = L1->next,rb = L2->next;
Linklist r = L1;
while(ra && rb){
if(ra->data <= L2->data){
r->next = ra; //尾插法
r = r->next;
ra = ra->next;
}
else{
r->next = rb;
r = r->next;
rb = rb->next;
}
}
while(ra){
r->next = ra;
r = r->next;
ra = ra->next;
}
while(rb){
r->next = rb;
r = r->next;
rb = rb->next;
}
r->next = NULL;
return L1;
}
3.7 将两个递增链表合并成一个递减链表
假设有两个按元素值递增次序排列的线性表,均以单链表形式存储。请编写算法将这两个单链表归并为一个按元素值递减次序排列的单链表,并要求利用原来两个单链表的结点存放归并后的单链表。
Linklist merge(Linklist L1,Linklist L2){
//合并两个递增有序单链表(带头结点),合并后链表递减排列
Linklist ra = L1->next,rb = L2->next;
Linklist r = L1,temp;
while(ra && rb){
if(ra->data >= L2->data){
temp = ra->next; //头插法
ra->next = r->next;
r->next = ra;
ra = temp;
}
else{
temp = rb->next; //头插法
rb->next = r->next;
r->next = rb;
rb = temp;
}
}
while(ra){
temp = ra->next;
ra->next = r->next;
r->next = ra;
ra = temp;
}
while(rb){
temp = rb->next;
rb->next = r->next;
r->next = rb;
rb = temp;
}
return L1;
}
3.8 判断一个链表是否对称
设计一个算法用于判断带头结点的循环双链表是否对称。
bool symmetry(Linklist L){
Linklist q = L->prior,p = L->next; //前后指针
while(q->next != p && p != q){ //表中元素为奇数/偶数
if(q->data != p->data)
return false;
p = p->next; //前指针后移
r = r->prior; //后指针前移
}
return true;
}3.9 依次输出链表中结点值最小的元素
设有一个带头结点的循环单链表,其结点值均为正整数。
设计一个算法,反复找出单链表中结点值最小的结点并输出,然后将该结点从中删除,直到单链表空为止,再删除表头结点。
void Delete_Min(Linklist &L){
Linklist p,ppre,minp,minpre;
while(L->next !=L ){ //表不空,循环
p = L->next;ppre = L; //ppre指向p前驱
minp = p;minpre = ppre;
while(p != L){ //循环一趟,寻找最小结点
if(p->data < minp->data){
minp = p;
minpre = ppre;
}
ppre = p;
p = p->next;
}
cout<<minp->data;
minpre->next = minp->next;
free(minp);
}
free(L);
}3.10 判断链表中是否存在环
经典的做法也是用快慢指针,如果没有环,快指针一定先到达链表的末端(NULL),如果有环,快、慢指针一定会相遇在环中.
检测环的入口:经典的做法是先检测是否有环,如果有环,则计算出环的长度,然后使用前后指针(不是快慢指针),所谓的前后指针就是一个指针先出发,走了若干步以后,第二个指针也出发,然后两个指针一起走,当前后指针相遇时,它们正好指向了环的入口.
Linklist FindLoopStart(Linklist head){
Linklist fast = head,slow = head;
while(fast!=NULL && fast->next!=NULL){
slow = slow->next;
fast = fast->next->next;
if(slow == fast) break; //相遇
}
if(slow==NULL || fast->next!=NULL)
return NULL; //没有环
Linklist p1 = head,p2 = slow;
while(p1 != p2){
p1 = p1->next;
p2 = p2->next;
}
return p1;
}4、真题
【2009统考真题】单链表 查找倒数第k个元素

【2012统考真题】找出单词相同后缀
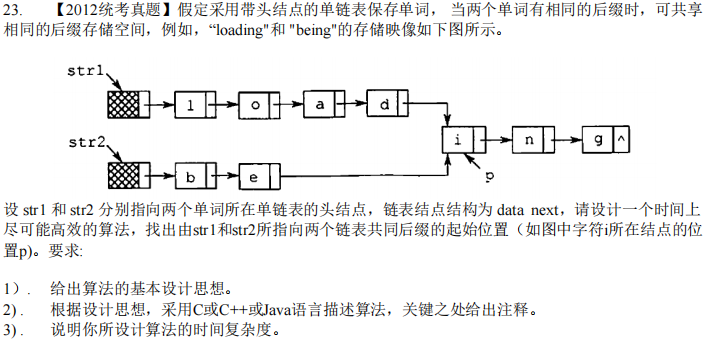
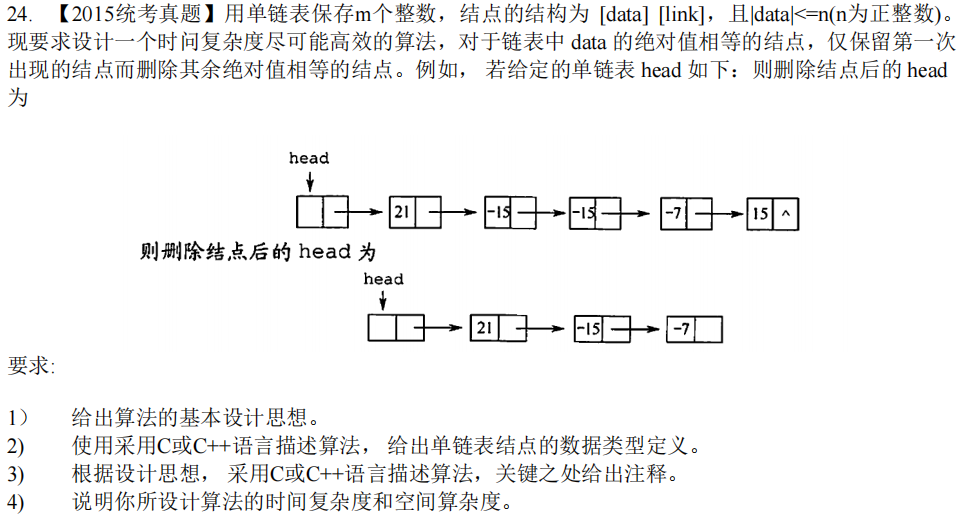
【2015统考真题】删除单链表绝对值相等结点
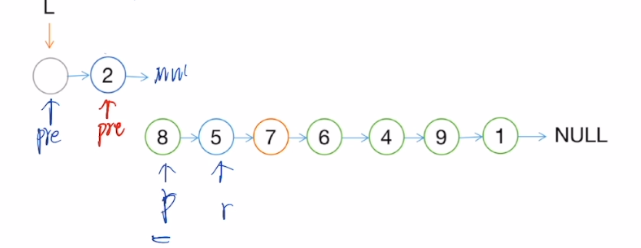
【2019统考真题】带头结点单链表+穿插+逆置

部分代码参考于
干货||链表的技巧和算法总结_指针
408数据结构学习强化——常见数据结构定义和算法总结_江南江南江南丶的博客-CSDN博客
【23考研】408代码题参考模板——链表_深海里的鱼(・ω<)★的博客-CSDN博客
