LC-6256. 将节点分成尽可能多的组(二分图判定+BFS)【周赛322】
6256. 将节点分成尽可能多的组
难度困难8
给你一个正整数 n ,表示一个 无向 图中的节点数目,节点编号从 1 到 n 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 双向 边。注意给定的图可能是不连通的。
请你将图划分为 m 个组(编号从 1 开始),满足以下要求:
- 图中每个节点都只属于一个组。
- 图中每条边连接的两个点
[ai, bi],如果ai属于编号为x的组,bi属于编号为y的组,那么|y - x| = 1。
请你返回最多可以将节点分为多少个组(也就是最大的 m )。如果没办法在给定条件下分组,请你返回 -1 。
示例 1:
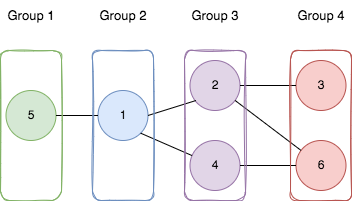
输入:n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
输出:4
解释:如上图所示,
- 节点 5 在第一个组。
- 节点 1 在第二个组。
- 节点 2 和节点 4 在第三个组。
- 节点 3 和节点 6 在第四个组。
所有边都满足题目要求。
如果我们创建第五个组,将第三个组或者第四个组中任何一个节点放到第五个组,至少有一条边连接的两个节点所属的组编号不符合题目要求。
示例 2:
输入:n = 3, edges = [[1,2],[2,3],[3,1]]
输出:-1
解释:如果我们将节点 1 放入第一个组,节点 2 放入第二个组,节点 3 放入第三个组,前两条边满足题目要求,但第三条边不满足题目要求。
没有任何符合题目要求的分组方式。
提示:
1 <= n <= 5001 <= edges.length <= 104edges[i].length == 21 <= ai, bi <= nai != bi- 两个点之间至多只有一条边。
二分图判定+BFS
题解:0x3f https://leetcode.cn/problems/divide-nodes-into-the-maximum-number-of-groups/solution/mei-ju-qi-dian-pao-bfs-by-endlesscheng-s5bu/
视频:https://leetcode.cn/link/?target=https://www.bilibili.com/video/BV15d4y147YF
class Solution:
def magnificentSets(self, n: int, edges: List[List[int]]) -> int:
# 建图
g = [[] for _ in range(n)]
for x, y in edges:
x -= 1
y -= 1 # 改成从0开始
g[x].append(y)
g[y].append(x)
# 由于需要执行多次bfs,在方法内开visit数组浪费空间复杂度
# 用clock 记录第几次遍历,time != clock 时说明这个点没有被访问
time = [0] * n
clock = 0
def bfs(start: int) -> int: # 返回最大编号
mx = 0 # 最大编号
nonlocal clock
clock += 1
time[start] = clock
q = deque([(start, base)]) # 初始化队列,存放开始和编号
while q:
x, id = q.popleft()
mx = max(mx, id)
for y in g[x]:
if time[y] != clock:
time[y] = clock
q.append((y, id+1))
return mx
color = [0] * n
def dfs(x: int, c: int) -> bool: # 染色法判定二分图
nodes.append(x)
color[x] = c # 0表示没有染色,1表示红色,-1表示蓝色
for y in g[x]:
if color[y] == c or color[y] == 0 and not dfs(y, -c):
return False
return True
ans = 0
for i,c in enumerate(color):
if c: # 如果已经被染色,直接continue
continue
nodes = []
if not dfs(i, 1): # 如果不是二分图,直接返回-1
return -1
# 是就开始分组
base = ans + 1 # 从上一次编号开始,因为求最大的分组
for x in nodes:
ans = max(ans,bfs(x))
return ans
