LALR(1)分析方法
LR(1)
分析法虽然可以解决一些
SLR(1)
方法无法解
决的冲突,但是对同一个文法而言,当向前看搜索
符不同时,
LR(1)
方法使同一个项目集分裂为多个
项目集,从而
导致状态数目增加
,
所需存储空间急剧增加。
为了克服
LR(1)
的这种缺点,考虑一种折衷的方法
――LALR(1)
方法
至于为什么使同一个项目集分裂为多个项目集这里给出一个文法就可以明白了
(0) S’→
S
(1) S→
BB
(2) B→
aB
(3) B→
b
我这里直接求出它的LR(1)分析项目集组 关于LR(1)文法的知识可以看LR(1)分析方法_用编程写诗的博客-CSDN博客
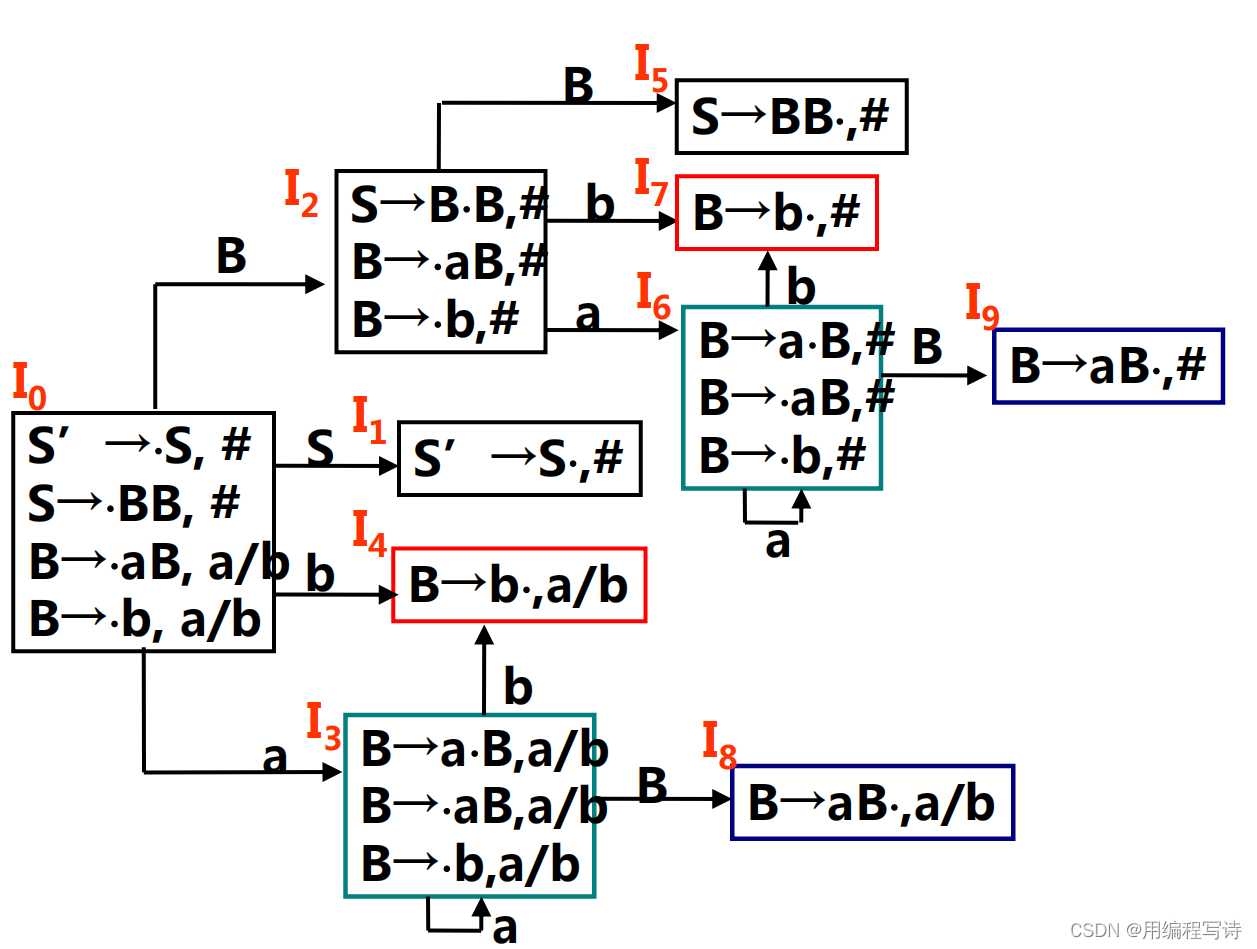
可以观察到其中
I
3
和
I
6,
I
4
和
I
7
,
I
8
和
I
9
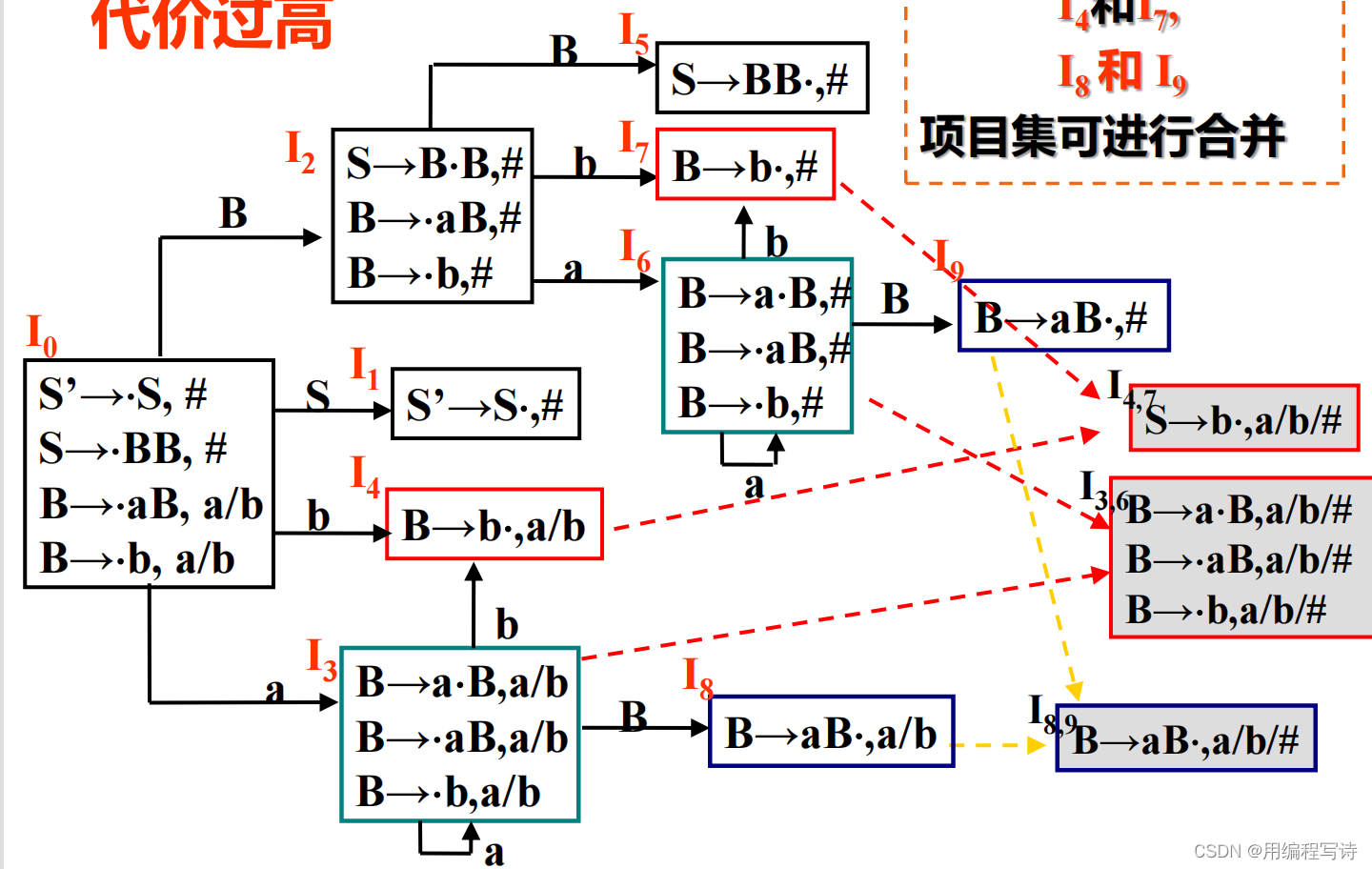
项目集可进行合并。我们可以看到这几个状态均是所有的项目是一样的但是他们的向前搜索符是不一样的。
我们可以得到合并之后的分析集组
对于同一个文法,
LR(1)
分析表和
LR(0)
以及
SLR
分析表永进具有相同数目的状态
LALR
方法本质上是一种折中方法,
LALR
分析表
比
LR(1)
分析表要小得多
,能力也差一点,但它却
能对付一些
SLR(1)
所不能对付的情况
LALR(1)分析(
LookAhead-LR
)基本思想
为了减少项目集的个数,将LR(1)项目集规范族中
的
同心集
合并,将其压缩为较小的
DFA
,若压缩过
程并未带来新的冲突,则分析表可大大地简化
所谓同心集是指搜索符不同而
LR(0) 项目(心)相
同
的 LR(1) 项目集
同心集合并后心仍相同,叧是超前搜索符集合为各同心集
超前搜索符的和集
合并同心集后转换函数自动合并
LR(1)文法合并同心集后也
只可能出现归约-归约冲突,而没有移进-归约冲突
构造
LALR(1)
分析表
构造
LR(1)
项目集规范族
C
= {
I
0
,
I
1
, …,
I
n
}
寻找
LR(1)
项目集规范族中同心的项目集,用它们
的并集代替它们
按构造规范的
LR(1)
分析表的方式进行构造
/
将
LR(1)
分析表合并
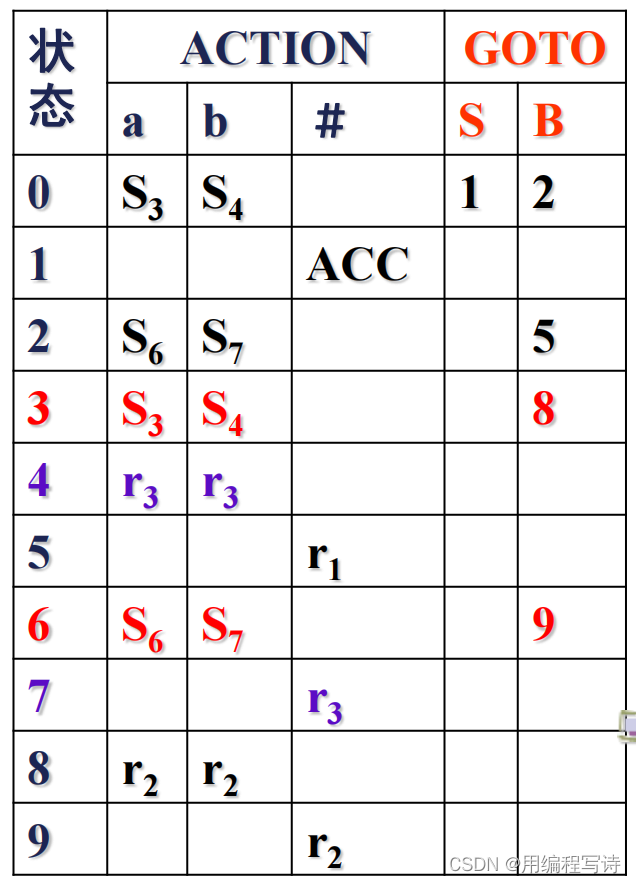
通过这样的方法可以看到:
原来的分析表
新的分析表:
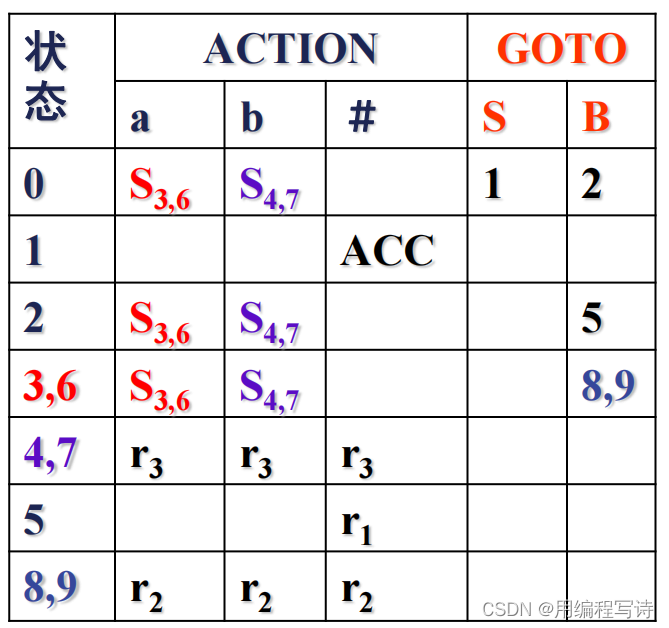
若构造的
LALR
分析表不存在冲突
,则该文法称为
LALR(1)
文法。
这里提醒一下,有一个很重要的事情:
合并同心项目集可能会引起冲突
同心集的合并不会引起新的移进-
归约冲突
同心集的合并有可能产生新的
归约-
归约
冲突
S’→
S
S→
aAd
|
bBd
|
aBe
|
bAe
A →
c
B →
c

合并同心集后

我们可以看到当我们碰到C之后向前搜索符都是d/e那么我们就不知道是规约到A或者B了。这里就会产生归约-归约冲突。
所以:该文法是
LR(1)
的,
但不是
LALR(1)
的。
