【完全背包】完全背包模板套用
1. 基础 —— 完全背包
- 经典问题:
背包容量为 4,有三件物品 [1, 15] [3, 20] [4, 30] ( [x, y] x为重量,y为价值)。物品可重复使用,请问背包中可装下的最大价值为多少?
- 状态转移方程:
dp数组含义 和 0-1背包中的 dp数组含义一样 ,都是表示当背包容量为 i 时,能装下的最大物品价值 ,状态转移方程为:
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
- 遍历方式:
看到这个状态转移方程你可能会疑惑,不是物品可以重复使用嘛,不是完全背包嘛,为什么状态转移方程和 0-1 背包(滚动数组形式)的状态转移方程一模一样?
答:完全背包和0-1背包的状态转移方程相同,只有遍历方式不同 ——
好的,这时我们就要仔细去思考一下了,当我们在解决 0-1 背包问题是如何遍历的 ?
如果你对 0-1 背包不理解,建议移步这篇文章 0-1背包介绍 ~~~
—— 从后往前遍历背包容量(当背包容量放不下物品 i 时,停止)。当时我们说为什么是从后向前遍历,且必须是从后向前遍历的原因你们还记得嘛? —— 对√,就是为了防止同一物品重复使用多次
完全背包和0-1背包的区别就在于完全背包可以重复使用元素,因此 —— 完全背包和 0-1 背包在代码上的区别也是完全背包要从前向后遍历背包容量 (从背包容量为物品 i 重量开始,到背包容量为最大背包容量结束)
理解了公式后,我们来填表,更好的体会一下这个过程:
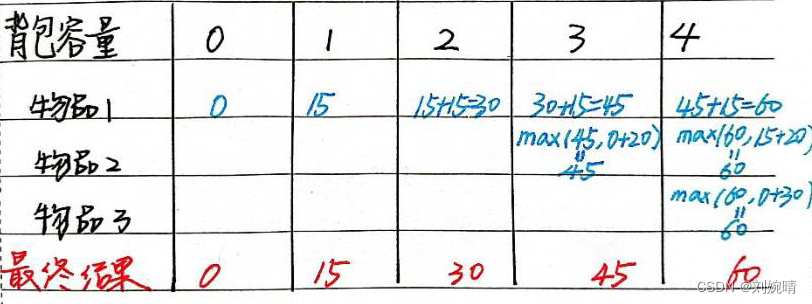
- 模板代码:
//先遍历物品,再遍历背包
private static void testCompletePack(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){ // 遍历物品
for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
// 完全背包问题
private static void testCompletePackAnotherWay(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
for (int j = 0; j < weight.length; j++){ // 遍历物品
if (i - weight[j] >= 0){
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
}
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
好了,理解了完全背包理论基础之后,让我们看一些变式题吧,都很简单的,直接套用模板就行了~~~
2. 变式题
- 变式题一:零钱兑换II
题目描述:
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。
链接:https://leetcode.cn/problems/coin-change-ii

思路:
我们可以把 amount 想象成背包容量,硬币想象成价值和重量相等的物品,这样这道题就转变成了往背包中装物品,装满的方式有多少的问题
-
dp数组含义 : 装满容量为 j ( 0<=j<=weight )的背包的方式数目
-
状态转移方程:
dp[j] += dp[j-coins[i]];装满问题的状态转移方程 几乎都是这样的,可以记忆一下,其含义为 装满容量为 j 的背包的方式数 等于不使用物品 i 的方式数 (dp[j]) 加上 使用物品 i 的方式数( dp[j-coins[i] )
-
遍历顺序问题:本题求的是组合,因此遍历顺序为外层 for 循环先遍历物品,内层 for循环后遍历背包容量
代码:
// 零钱兑换问题
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] = 1;
for(int i=0; i<coins.length; i++){
for(int j=coins[i]; j<=amount; j++){
dp[j] += dp[j-coins[i]];
}
}
return dp[amount];
}
变式二: 组合总和
题目:
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。
链接:https://leetcode.cn/problems/combination-sum-iv

思路:
本题和上述零钱问题差不多,只是遍历顺序有所改变,本题的话 [1,1,2] 和 [1,2,1] 算作不同的结果。因此遍历顺序为先遍历背包容量,再遍历物品。
为什么是这种顺序:
假设我们先遍历物品那么物品 1 一定在 物品 2 之前,物品 2 一定在物品 3 之前。就一定不会出现 [3,2] 这种结果,因此要内层循环后遍历物品,外层循环先遍历背包容量
填表加强理解:

代码:
// 组合总数
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
dp[0] = 1;
for(int i=1; i<target; i++){ // 背包容量
for(int j=0; j<=nums.length; j++){ // 物品
if(nums[j] <= i){
dp[i] += dp[i-nums[j]];
}
}
}
return dp[target];
}
变式三: 零钱兑换
题目描述:
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。
链接:https://leetcode.cn/problems/coin-change
思路:
- 本题与 零钱兑换II 的区别: 零钱兑换二求取的是装满背包情况的组合数,本题求取的是装满背包需要的最少硬币数量,明确了这点之后我们就可以去向 dp 数组的含义了
- dp[] 数组表示装满容量为 j 的背包需要的最少硬币数量
- 状态转移方程为
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
含义解释:表示装满容量为 j 的背包需要的最少硬币数量为 最小的 装满容量为( j - coins[i] )的背包需要的硬币数量再加一,即装满容量为( j - coins[i] )的背包再加上当前硬币 - 初始化: dp[0] = 0 表示装满容量为0的背包,不需要物品 。j != 0 时,值初始化为整数最大值,防止在计算
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);时,dp[j - coins[i]] + 1被淹没
代码:
// 零钱兑换 —— 装满背包所用的最少硬币数量
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
Arrays.fill(dp, Integer.MAX_VALUE); // 用最大整数填充数组,防止被淹没
dp[0] = 0; // 装满容量为0的背包不需要物品
for(int i=0; i<coins.length; i++){
for(int j=coins[i]; j<=amount; j++){
if(dp[j-coins[i]] != Integer.MAX_VALUE) {
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount];
}
变式题四 - 完全平方数
题目描述:
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
链接:https://leetcode.cn/problems/perfect-squares
示例:

思路:
看了这么多背包问题,小白已经对此很熟悉了,本题转换成背包,就是完全平方数(1,4,9,16…)是物品,总和 n 是背包容量。但是小白还是有一点疑惑的地方,完全平方数怎么表示鸭,是不是要建立一个 value 数组,把完全平方数都放进去。
当我想到这一点时,我就已经掉入了完全套模板学习的僵化的思维中了。当然,作为一个小白我认为这不可耻,让我来从源头分析一下,之前我们要把物品放进数组中的原因是什么 —— 因为物品元素值随机无法表示。
而本题的完全平方数与下标i具有明显关系 :完全平方数 = i * i ( i >=1 && i * i <= n) ,因此我们只需要遍历 i 即可,物品用 i * i 表示,完全不需要再设立一个数组,放完全平方数了。
代码:
// 完全平方数
public int numSquares(int n) {
int[] dp = new int[n+1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for(int i=1; i*i<=n; i++){ // 遍历物品 物品为 1*1 , 2*2, 3*3 ...(i * i <= n)
for(int j=1; j<=n; j++){
if(j >= (i*i)){ //j >= (i*i) 才有意义
dp[j] = Math.min(dp[j], dp[j - i*i] + 1);
}
}
}
return dp[n];
}
变式题5 - 单词拆分
题目描述:
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
链接:https://leetcode.cn/problems/word-break
思路:
把本题想成背包还是挺难的,估计还需要多加训练,将单词看作物品,字符串 s 看作背包,将单词装进背包中
- dp 数组含义 : dp 数组表示,容量为 i 的背包是否可以被单词装好,若可以为 true,若不可以为 false
- 状态转移方程 dp[i] = dp[i-len] (len 为单词 j 的长度 , 且
wordDict[j].equals(s.substring(i-len, i))
含义:当单词 j 正好匹配s.substring(i-len, i)时,容量为 i 的背包能否被装好,由容量为 i-len 的背包决定,即容量为 (i-len)的背包再装单词 j 即可装好 - dp 初始化,因为全部其他值都需要由dp[0] 退出,因此初始化 dp[0] = true
代码:
// 单词拆分
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp = new boolean[s.length()+1];
dp[0] = true;
for(int i=1; i<=s.length(); i++){
for(int j=0; j<wordDict.size(); j++){
int len = wordDict.get(j).length();
if(i>=len && wordDict.get(j).equals(s.substring(i-len, i))){
dp[i] = dp[i-len];
if(dp[i-len]) {
break;
}
}
}
}
return dp[s.length()];
}
尾注:完全背包就暂时告一段落了~~
PS: 为什么要写文章,写文章很累,但是不想浑浑噩噩的以为自己会了,其实根本就是囫囵吞枣,写出来会发现很多不一样的细节,费曼学习法是一种很好的学习方法。加油吧,少年!!!
