Treap树堆
1.概念
当串行一直插入连续的数字,会导致树成为一个链表,时间复杂度变为0N
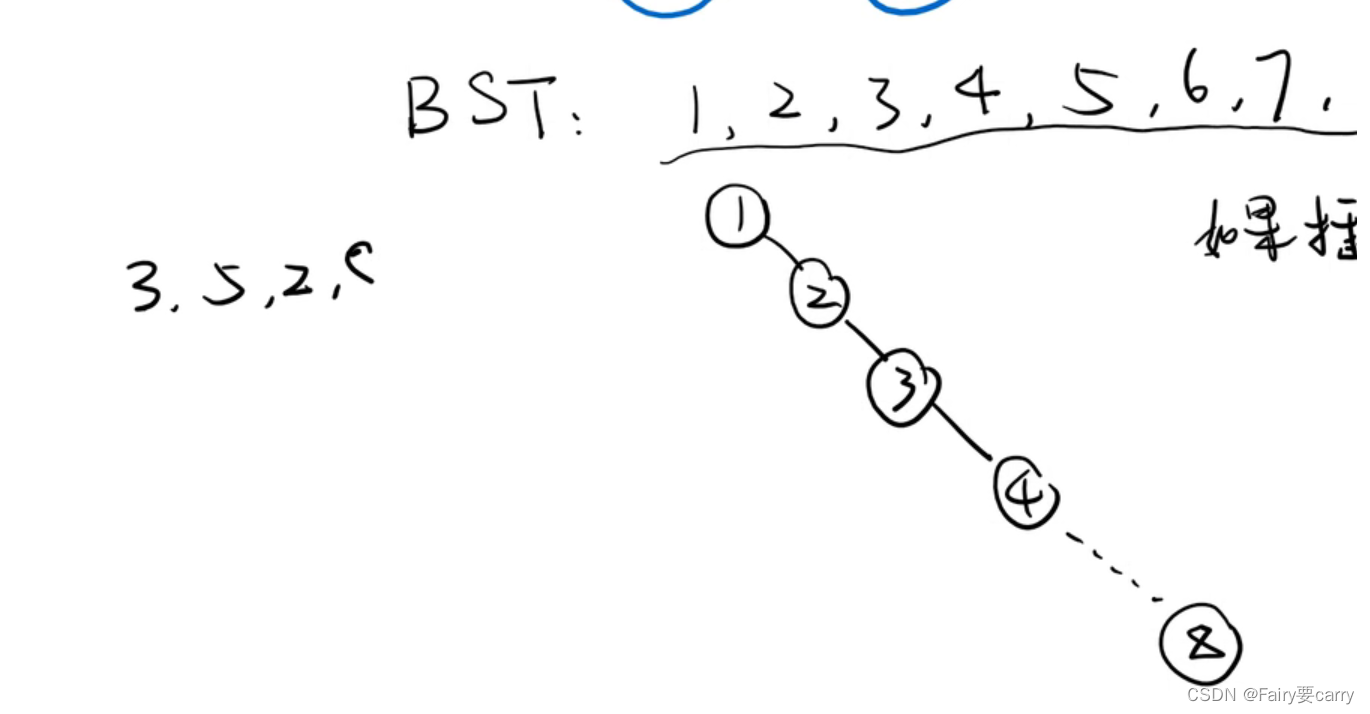
树堆概念:
主要体现的思想是随机插入数字,会给每个数字赋予一个优先级——>目的是让插入的关键字满足二叉树(节点的性质满足=(关键字:优先级))
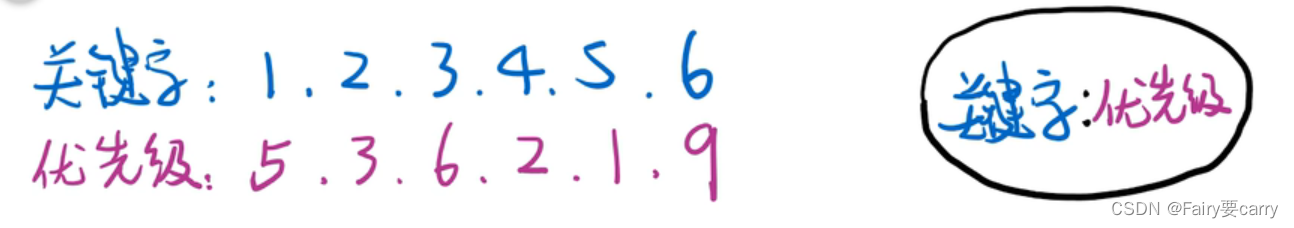
树堆=二叉搜索树+堆
1.首先按照关键字插入,1插入,然后插入关键字2并记录优先级,2<1理当2在1的右边
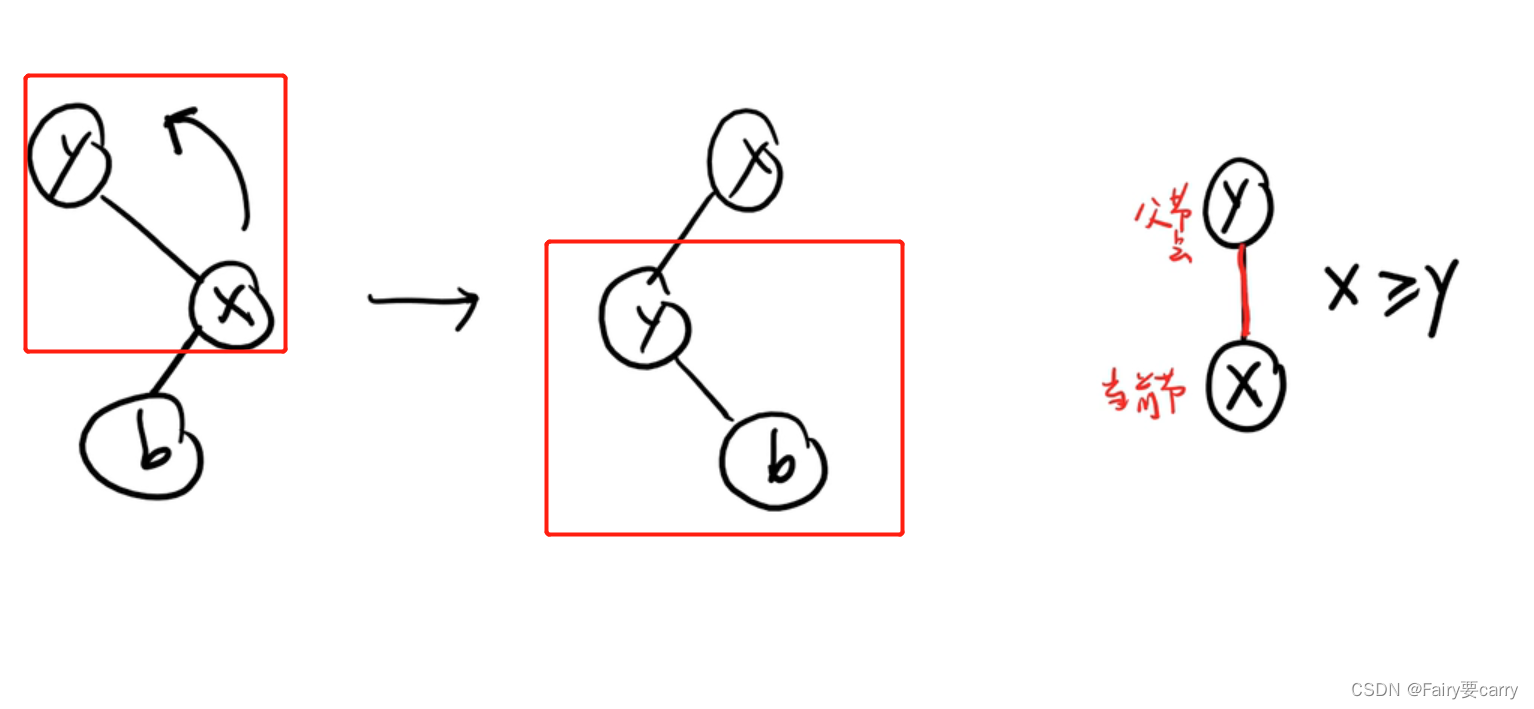
2.后面发现关键字2的优先级<1的优先级,所以2需要上浮满足小顶堆**(左旋上浮)**
特点:被旋转的节点的左子树会到原父节点的右子树上(节点左旋,那么节点的右子树还是一直挂着保护着的)
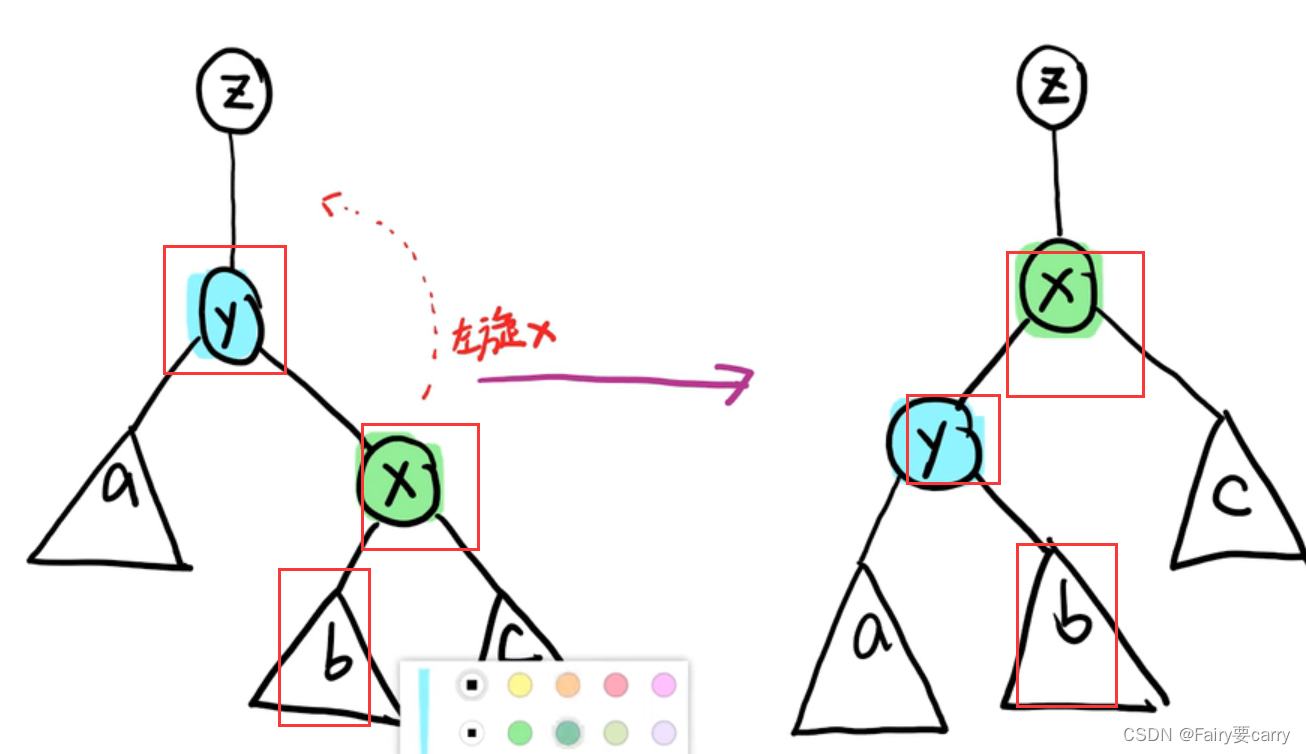
左旋右旋
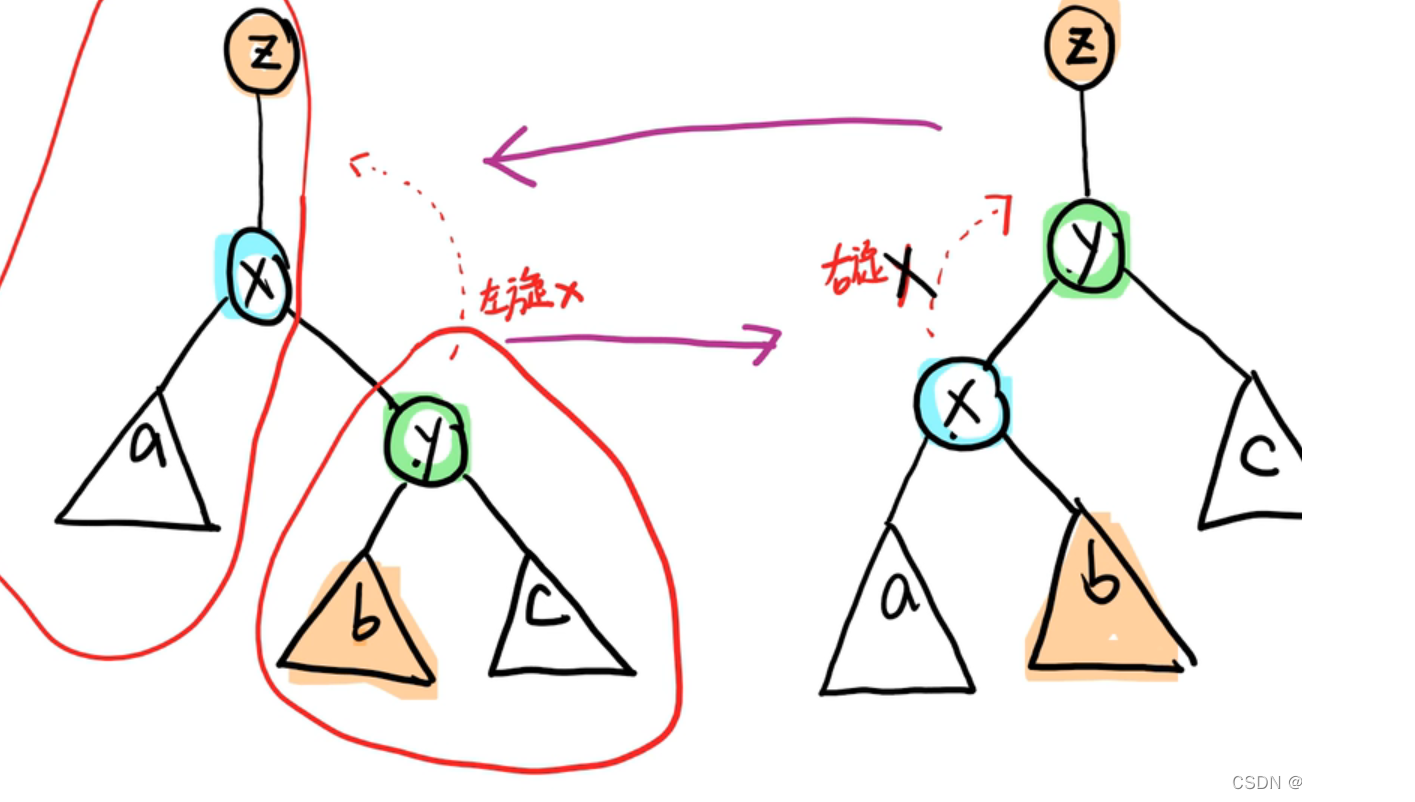
有点像生活现象:
新来的员工比老员工工作积极亢奋,就会往上冲去比较优先级,而老的就大多就安于现状所以不会网上冲了
如果插入顺序是随机的,则一颗二叉搜索树的深度是解决0(logn)的
我们可以按照优先级进行排序,然后再按照树那样进行插入(按照树堆的方式进行插入)
时间复杂度(深度-0(h)插入+0(h)左旋):h-0(log2n);
如何左旋:选择一个较小优先级的叶子节点,然后与父节点进行交换即可
如何插入
- 按照二叉查找树的插入方式,将节点插入到树叶中
- 再按照priority项的堆序(小顶堆)性质进行节点位置的调整
如何删除
将要删除的节点与最后一个节点交换,然后删除最后叶子节点即可,最后将树下沉保证堆的性质
- 找到相应的结点
- 若该结点为叶子结点,则直接删除;
若该结点为非叶子节点,则进行相应的旋转,直到该结点为叶子节点,然后进行删除。
优缺点
- Treap简明易懂。Treap只有两种调整方式,左旋和右旋。
- Treap易于编写。Treap只需维护一个满足堆序的修正值,修正值一经生成无需修改。
- Treap稳定性佳。Treap的平衡性虽不如 AVL,红黑树, SBT等平衡树,但是 Treap也不会退化,可以保证期望 O(logN)的深度。Treap的稳定性取决于随机数发生器。
- Treap具有良好的实践效果。各种实际应用中, Treap的稳定性表现得相当出色,没有因为任何的构造出的数据而退化。
- Treap像跳跃表一样使用了随机数,使Treap树的深度为O(logN),所以对于任意的输入其操作的时间复杂度都为O(logN)。
- 查找操作的时间等同于非平衡二叉查找树,所以比平衡二叉查找树要慢
- 插入操作的时间只比递归非平衡二叉查找树稍慢。
- 删除操作的时间虽然也要慢的多,但也是O(logN)。
差异
相当于普通BST的进化版,在此基础上加了堆的性质保证平衡(满足大根堆或者小根堆)
2.代码实现
package chapter12;
import chapter04.MyCustomException;
import java.util.Random;
public class Treap<T extends Comparable<? super T>> {
private Node<T> root; // 根节点
private final Node<T> nullNode; // 空节点
private static class Node<T> {
static Random random = new Random(); // 随机数发生器
T element; // key值
int priority; // 优先级
Node<T> left;
Node<T> right;
Node(T element) {
this(element, null, null);
}
Node(T element, Node<T> left, Node<T> right) {
this.element = element;
this.priority = random.nextInt();
this.left = left;
this.right = right;
}
}
// ************************************************************************************************************
public Treap() {
nullNode = new Node<>(null);
nullNode.left = nullNode.right = nullNode;
nullNode.priority = Integer.MAX_VALUE;
root = nullNode;
}
public void makeEmpty() {
root = nullNode;
}
public boolean isEmpty() {
return root == nullNode;
}
public void insert(T element) {
root = insert(element, root);
}
public void remove(T element) {
root = remove(element, root);
}
public boolean contains(T element) {
Node<T> current = root;
nullNode.element = element;
while (true) {
int compareResult = element.compareTo(current.element);
if (compareResult < 0)
current = current.left;
else if (compareResult > 0)
current = current.right;
else
return current != nullNode;
}
}
public T findMin() {
if (isEmpty()) {
throw new MyCustomException();
}
return findMin(root).element;
}
public T findMax() {
if (isEmpty()) {
throw new MyCustomException();
}
return findMax(root).element;
}
public void printTree() {
printTree(root);
}
// ************************************************************************************************************
/**
* treap的插入操作:
* 1.按照二叉查找树的插入方式,将节点插入到树叶中
* 2.再按照priority项的堆序(小顶堆)性质进行节点位置的调整
*
* @param element:要插入的元素
* @param node:本节点
*/
private Node<T> insert(T element, Node<T> node) {
if (node == nullNode) {
return new Node<>(element, nullNode, nullNode); // 插入到叶子节点中
}
int compareResult = element.compareTo(node.element);
if (compareResult < 0) {
node.left = insert(element, node.left); // 按二叉查找树的性质插入
if (node.left.priority < node.priority) { // 按priority的堆序性质(小顶堆)进行调整
node = rotateWithLeftChild(node);
}
} else if (compareResult > 0) {
node.right = insert(element, node.right);
if (node.right.priority < node.priority) {
node = rotateWithRightChild(node);
}
}
return node;
}
// 左一字型的单旋转
private Node<T> rotateWithLeftChild(Node<T> t) {
Node<T> tmp = t.left;
t.left = tmp.right;
tmp.right = t;
return tmp;
}
// 右一字型的单旋转
private Node<T> rotateWithRightChild(Node<T> t) {
Node<T> tmp = t.right;
t.right = tmp.left;
tmp.left = t;
return tmp;
}
/**
* treap的删除操作:
* 1.找到相应的结点
* 2.若该结点为叶子结点,则直接删除;
* 若该结点为非叶子节点,则进行相应的旋转,直到该结点为叶子节点,然后进行删除。
*
* @param element:要删除的元素
* @param node:本节点
*/
private Node<T> remove(T element, Node<T> node) {
if (node != nullNode) {
int compareResult = element.compareTo(node.element);
if (compareResult < 0) {
node.left = remove(element, node.left);
} else if (compareResult > 0) {
node.right = remove(element, node.right);
} else { // compareResult = 0,即找到对应项
if (node.left.priority < node.right.priority) {
node = rotateWithLeftChild(node);
} else {
node = rotateWithRightChild(node);
}
if (node != nullNode) { // 如果node不是nullNode,则说明未旋转之前的node不为树叶,需要将之前的node往树叶处旋转,然后在进行删除
node = remove(element, node);
} else {
node.left = nullNode; // 如果node是nullNode,则说明未旋转之前的node为树叶,可以直接删除。
}
}
}
return node;
}
private Node<T> findMin(Node<T> node) {
if (node.left == nullNode) {
return node;
} else {
return findMin(node.left);
}
}
private Node<T> findMax(Node<T> node) {
if (node.right == nullNode) {
return node;
} else {
return findMin(node.right);
}
}
private void printTree(Node<T> node) {
if (node != nullNode) {
printTree(node.left);
System.out.println(node.element);
printTree(node.right);
}
}
// ************************************************************************************************************
public static void main(String[] args) {
Treap<String> treap = new Treap<>();
treap.insert("GG");
treap.insert("TT");
treap.insert("OO");
treap.insert("BB");
treap.insert("NN");
treap.insert("LL");
treap.insert("GG");
treap.insert("UU");
treap.printTree();
treap.remove("GG");
treap.remove("TT");
treap.remove("OO");
treap.remove("BB");
treap.remove("NN");
treap.remove("LL");
treap.remove("UU");
treap.printTree();
treap.insert("AA");
System.out.println();
System.out.println(treap.root.element);
}
}
