曲率

比如我们想知道曲线 $\mathbf{AB}$ 上任一点处的弯曲程度怎么办呢？这时就需要一个十分重要的概念——曲率。

维基百科：

• 在数学中，曲率（curvature）是描述几何体弯曲程度的量，例如曲面偏离平面的程度，或者曲线偏离直线的程度。在不同的几何学领域中，曲率的具体定义不完全相同。曲率可分为外在曲率和内蕴曲率，二者有重要的区别。前者的定义需要把几何体嵌入到欧式空间中，后者则是直接定义在黎曼流形上。
• 曲线的曲率通常是标量，但也可以定义曲率向量。对于更复杂的对象（例如曲面，或者一般的 n 维空间），曲率要用更复杂的线性代数来描述，例如一般的黎曼曲率张量。

曲率包含的知识点很多，如下所示：

1.1 弧长参数 s

弧长参数又称为自然参数，该参数的引入是意义非凡的。一个最为明显的意义在于，弧长作为参数就是将参数赋予了几何意义，这样在几何意义上，就可以将参数和曲线本身统一起来。

那么现在就有一个问题了，为什么弧长可以作为参数？ 说明这个问题之前我们需要先知道如何求一条曲线的弧长。

设： $C^1$ 类曲线的参数方程为：

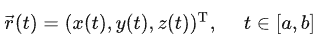
注：$C^1$ 类曲线是指光滑曲线。

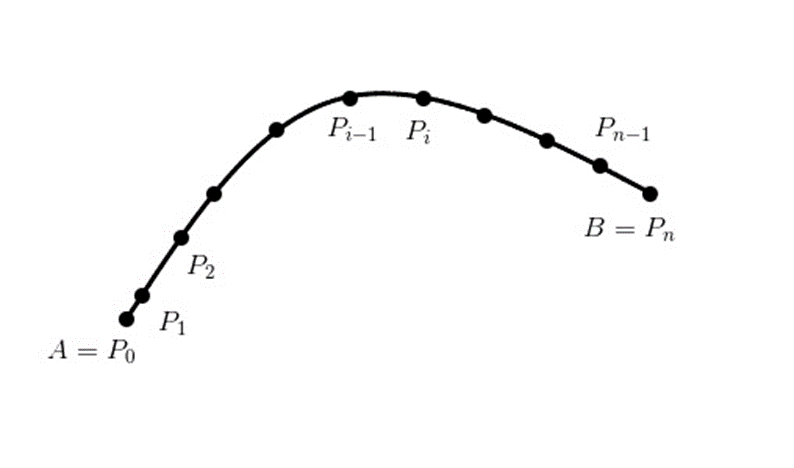
我们按照上面的方式划分为 $n$ 个小段，之后我们用直线将相邻的两个点连结起来，最后会得到一条折线，这条折线的长度记为：

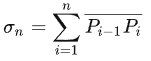
取 λ n = max ⁡ a ≤ t ≤ b { t i − t i − 1 } \lambda_n=\max_{a\leq t\leq b}\{t_i-t_{i-1}\} λn​=maxa≤t≤b​{ti​−ti−1​}，并使 ${\lim }_{n\to +\infty }{\lambda }_n=0$，此时 ${\sigma }_n$ 趋于一共与分点无关的确定的极限 $\sigma$ ，这个极限我们就定义为曲线 $P_0{P}_n$ 的长度，即：

参考资料

[1] 什么是曲率？什么又是挠率？2019.7