差分法逼近微分

背景引入

几乎所有的机器学习算法在训练或者预测式都是求解最优化问题。因此需要依赖微积分求解函数的极值。而差分法（Difference Method）则是一种常见的求解微分方程（Difference Equation）数值解的数学方法。

差分法简介

差分法主要通过有限差分来近似表示导数（Derivative），从而寻找微分方程的近似解。换而言之，差分法是用有限差分来代替微分，用有限差商（Finite Difference Quotient）来替代导数，从而把基本方程和边界条件（一般均为微分方程）近似地转化为差分方程（代数方程）来表示，把求解微分方程的问题转化为求解代数方程的问题。有限差分导数的逼近（Approximation）在微分方程数值解的有限差分方法中，特别是边界值问题中，骑着关键的作用。
有限差分则是形式为f（x+b）-f(x+a)的数学表达式，若有限差分除以（b-a），则得到差商，亦即倒数的近似值。设所有x的解析函数y=f（x），函数y对x的导数为：
dy/dx=lim（Δy/Δx）=lim((f(x+Δx)-f(x))/Δx) Δx->0
其中，dy,dx分别为函数及自变量的微分，dy/dx是函数对自变量的导数，又称为微商（Differential Quotient）Δy，Δx则分别称为函数及自变量的差分，而Δy/Δx则为函数对自变量的差商。由导数（微商）和差商的定义可知，当自变量的差分（增量）趋近于0时，就可由差商得到导数。因此，在数值计算中，常以差商替代导数。

差分的不同形式及其代码实现

差分有3种形式：向前差分，向后差分以及中心差分。
我们以一阶差分为例：
向前差分：Δpy=f（x+Δpx）-f（x）
向后差分：Δy=f（x）-f（x-Δx）
中心差分：Δy=f（x+Δx）-f（x-Δx）
与其对应的一阶差商如下。
向前差商：
Δy/Δx=（f（x+Δx）-f（x））/Δx
向后差商：
Δy/Δx=（f（x）-f（x-Δx））/Δx
中心差商：
Δy/Δx=（f（x+Δx）-f（x-Δx））/Δx
以下示例代码展示了函数f（x）几种不同的差商形式：

#差分法逼近微分
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签

#定义函数
f=lambda x:5*x**3+2*x**2+7

#返回向前差商
def forward_diff(x,h):
    plt.plot([x,x+h],[f(x),f(x+h)],'b-d',label='向前差商')
    return (f(x+h)-f(x))/h
#返回向后差商
def backward_diff(x,h):
    plt.plot([x-h,x],[f(x-h),f(x)],'r*-',label='向后差商')
    return (f(x)-f(x-h))/h

#返回中心差商
def central_diff(x,h):
    a=(f(x-h)+f(x+h))/2
    plt.plot([x-h,x+h],[f(x-h)+f(x)-a,f(x+h)+f(x)-a],'g--',label='中心差商')
    return (f(x+h)-f(x-h))/(2*h)
xx=np.linspace(-1.0,1.5,20)  #产生等差数列作为坐标轴标记
yy=f(xx)
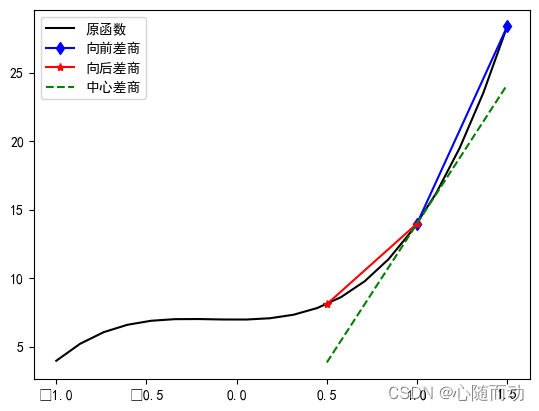
plt.plot(xx,yy,'k-',label='原函数')
print('向前差商',forward_diff(1,0.5))
print('向后差商',backward_diff(1,0.5))
print('中心差商',central_diff(1,0.5))
plt.legend()
plt.show()

结果展示：
向前差商 28.75
向后差商 11.75
中心差商 20.25

蒙特卡罗方法

背景引入

著名的人工智能“AlphaGo”因其在与多位世界级围棋大师对战中的出色表现而声明鹊起。除了卷积神经网络（Convolutional Neural Networks，CNN）技术的应用外，基于蒙特卡罗数的搜索方法等技术手段也在其中起了关键性的作用。蒙特卡罗方法(Monte Carlo Method)称为统计模拟方法，是一种以概率统计理论为指导的一类非常重要的数值计算方法。它诞生于20世纪40年代美国著名的曼哈顿计划（Manhattan Project），由该计划中的成员————计算机之父约翰·冯·洛依曼（John von Neumann）与数学家S.M.乌拉姆(Stanislaw Marcin Ulam )首先提出并以世界著名的赌城摩纳哥的蒙特卡罗来命名。

蒙特卡罗方法原理

蒙特卡罗法 是一种用来模拟随机现象的数学方法，这种方法在作战模拟中能直接反映作战过程中的随机性。在作战模拟中能用解析法解决的问题虽然越来越多，但有些情况下却只能采用蒙特卡罗法 。使用蒙特卡罗法 的基本步骤如下：
(1)根据作战过程的特点构造模拟模型；
(2)确定所需要的各项基础数据；
(3)使用可提高模拟精度和收敛速度的方法；
(4)估计模拟次数；
(5)编制程序并在计算机上运行；
(6)统计处理数据，给出问题的模拟结果及其精度估计。
在蒙特卡罗法 中，对同一个问题或现象可采用多种不同的模拟方法，它们有好有差，精度有高有低，计算量有大有小，收敛速度有快有慢，在方法的选择上有一定的技巧。
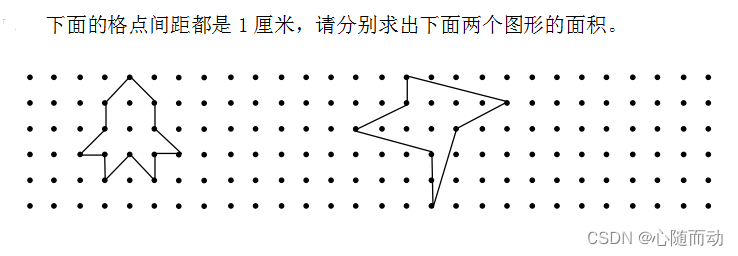
例如，在求不规则的图形的面积的时候，使用蒙特卡罗方法近似求解可以很方便的求解面积。假设图中的正方形边长为1，S1和S2分别表示不同图形的面积与正方形的面积，N1，N2分别表示落在不规则图形的随机点数以及所有随机点数。
S1/N1=S2/N2

蒙特卡罗方法应用

蒙特卡罗方法可应用于多种场合，但求出的解为近似解，在摸样样本数越大的情况下，结果越接近真实值，不过，样本数的剧增也会导致计算量的大幅上升。下面我们通过几个实例来说明蒙特卡罗方法的一些简单应用。

计算圆周率

假设有一个边长未为2的正方形，则其面积S1=2x2=4，其内接圆的半径为r=1，类结缘的面积为S2=Π*r²=Π。那么S1/S2=Π/4.
基于蒙特卡罗方法计算圆周率的示例代码：

import numpy as np
r=1  #定义内接圆半径
rand_num=[100,1000,10000,100000,1000000,10000000]
for N in rand_num:
    #在边长为2的正方形区域生成随即点坐标（x,y）
    x=2*np.random.random_sample(N)-1
    y=2*np.random.random_sample(N)-1
    in_circle_point_num=0
    #计算落在内接圆区域里的随机点数
    for point_count in range(len(x)):
        #判断随机点时否落在类结缘区域之内
        if(x[point_count]*x[point_count]+y[point_count]*y[point_count]<r*r):
            in_circle_point_num+=1
    print('N=',str(N),'pi=',str(4.0*in_circle_point_num/N))

结果展示：
N= 100 pi= 2.68 N= 1000 pi= 3.176 N= 10000 pi= 3.1316 N= 100000 pi= 3.13248 N= 1000000 pi= 3.13982 N= 10000000 pi= 3.141796

计算定积分

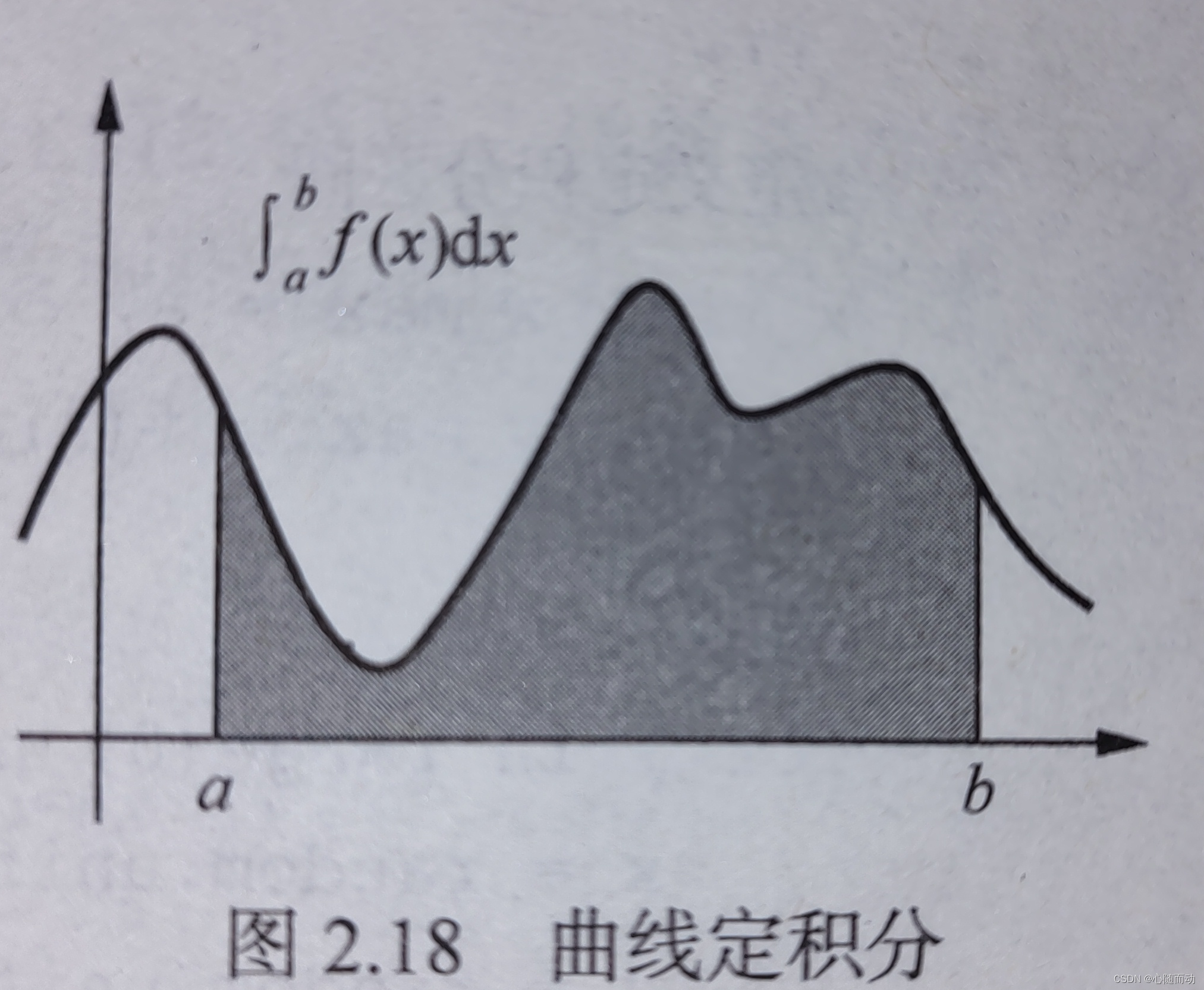
例如像上例图像，用随即点模拟的方式来近似计算定积分的值。采用蒙特卡罗方法，在该矩形区域内产生大量的随机点（例如N），计算落在阴影区域内的随机点数（counts）。那么其积分的近似值则为（counts/N）24.
以下即为上述基于蒙特卡罗方法计算定积分的示例代码：

import random
import numpy as np
import scipy.integrate as integrate

def MonteCarlo_Integral(f,a,b,n):
    '''
    基于蒙特卡罗方法计算定积分
    F:定积分曲线方程
    a，b：区间[a,b]
    n:产生随机点数
    '''
    #定义定积分区间
    x_min,x_max=a,b
    y_min,y_max=f(a),f(b)

    count=0
    for i in range(0,n):
        x=random.uniform(x_min,x_max)
        y=random.uniform(y_min,y_max)
        #判断条件y<f(x)表示该随即点位于曲线下方
        if(y<f(x)):
            count+=1
    integral_value=(count/float(n))*f(a)*f(b)
    print(integral_value)
if __name__=='__main__':
    #产生8个随机点数
    N=10000
    #定积分曲线
    f=lambda x:x**2
    #利用蒙特卡罗方法计算定积分
    MonteCarlo_Integral(f,0,2,N)
    #利用scipy内置模块直接计算定积分
    print(integrate.quad(f,0,2))

计算结果：
0.0 (2.666666666666667, 2.960594732333751e-14)
该结果存在一定误差，样本数越大，则误差越小。

梯度下降算法

算法简介

梯度下降（Gradient Descent）是一种求局部最优解的优化算法。在求解机器学习算法的模型参数即无约束优化问题，梯度下降是常用方法之一，主要用来递归性地逼近最小误差模型。

方向导数与梯度

在学习梯度下降算法之前，我们需要先了解梯度(Gradient)的概念。在此之前，我们先来回顾一下什么方向导数及其几何意义。

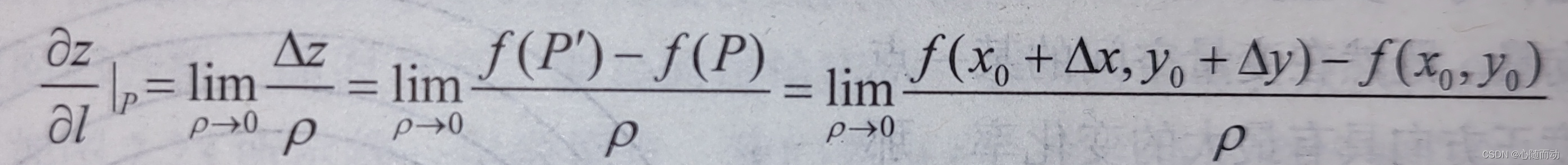
图形解释：

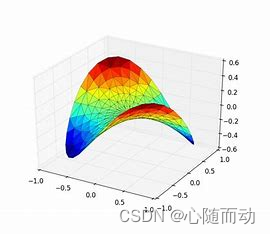
对于导数以及偏导数的定义，均为沿坐标轴正方向函数的变化率。当我们讨论函数沿任意方向的变化率，就引出了方向导数的定义，即某一点在某一方向上的导数值。

梯度下降

梯度下降，又名最速下降（Steepest Descent），是求解无约束最优化问题最常用的方法。它是一种迭代方法，每一步主要的操作是求解目标函数的梯度向量。既然在向量空间的某一点处，函数沿梯度正方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着梯度负方向去减少函数值，以此达到我们的优化目标。因为在梯度负方向上目标函数下降最快，这也是最速下降名称的由来。梯度下降法特点为越接近目标值步长越小，下降速度越慢。如图，每一个圈代表一个函数梯度，其中心位置表示函数极值点。每次迭代根据当前位置求得的梯度（用于确定搜索方向以及与步长共同决定前进速度）和步长找到一个新位置，这样不断迭代最终到达目标函数局部最优点（如果目标函数是凸函数，则到达全局最优点）。

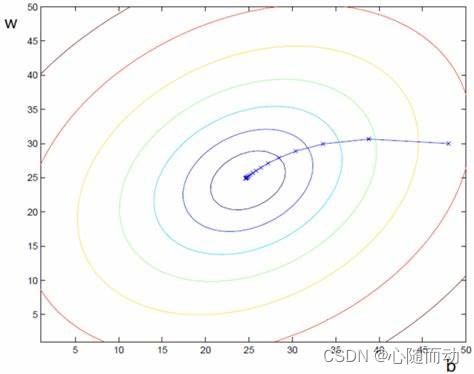
上述梯度下降过程可描述为一个函数自变量的迭代过程，用一个数学公式描述如下：
β=β-α·▽J（o）
其中，J为关于o的函数，β为当前所处位置，从该位置沿着下降最快的方向，即为梯度负方向-▽j（o），移动前进至β（i+1），α为每次的移动步长。重复该步骤直至抵达函数J的极值点。梯度下降中的α在机器学习中也被称为学习率（Learning Rate）或步长，通过α来控制每一步的距离，既要保证不让步长大大错过最低点，也要保证让步长太小而导致学习速度过慢而影响整体效率。

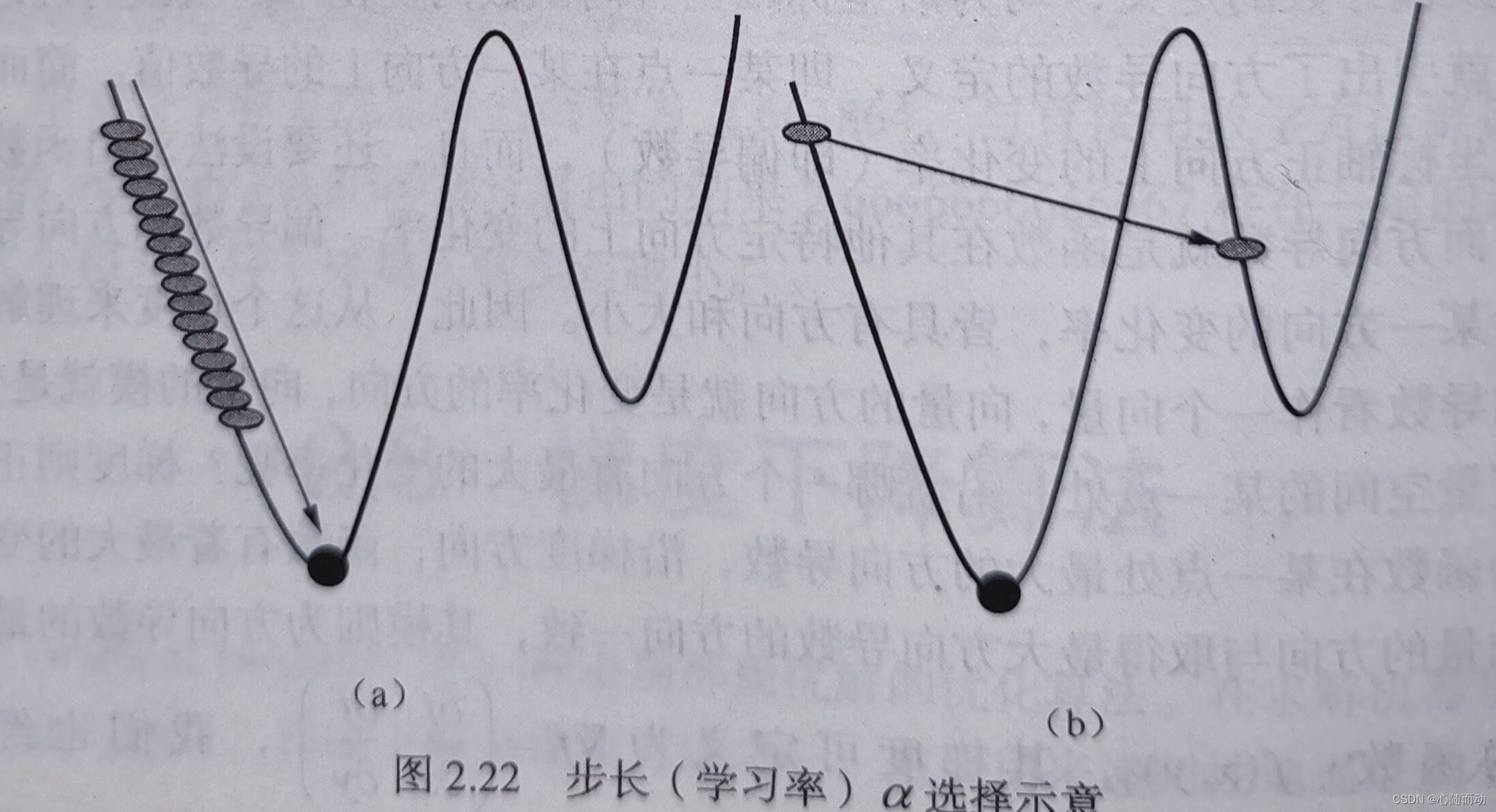
基于梯度下降算法的线性回归

在统计学中，线性回归（Linear Regression）是利用线性回归方程对一个或多个自变量与因变量之间的关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。在回归分析中，只包含一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析包含两个或两个以上的自变量，且因变量和自变量之间存在线性关系，则称为多元线性回归分析。
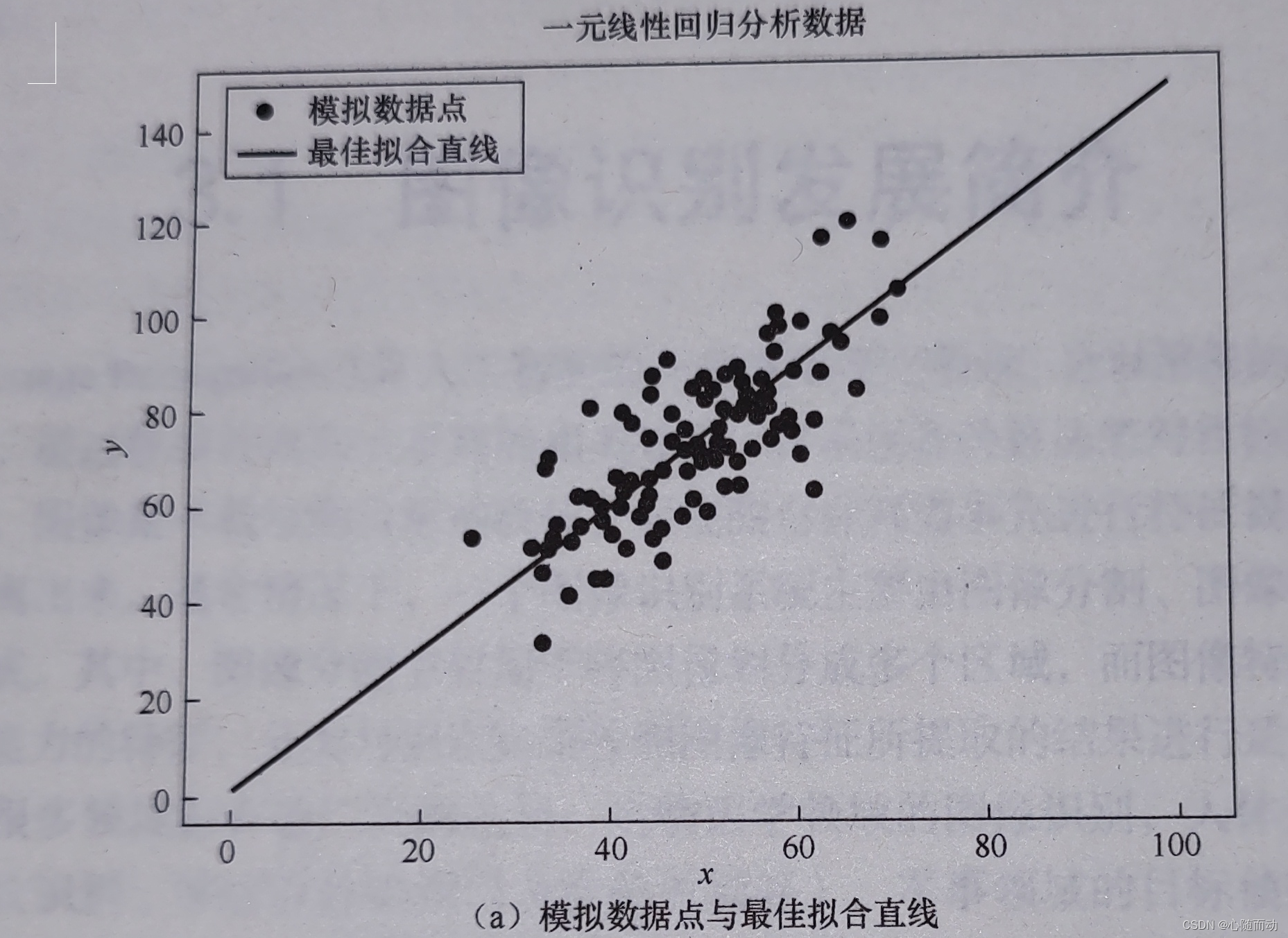
一元线性回归分析，简而言之，就是通过给定的一系列数据点，求出符合这些点的最佳直线方程。假设有如图的一组数据点，我们要找到一条合适的直线来拟合这些数据。为此，我们将使用标准的y=mx+b直线方程，其中m为直线的斜率（Slope），b为直线的y轴截距（Intercept）。想要找到最佳的数据拟合直线，只需找到m与b最佳的值即可。

解决这类问题的标准方法是，首先定义一个误差函数，亦可称为代价函数或成本函数（Cost Function），用于评估函数与数据点之间的拟合程度。误差函数的值越小，代表模型拟合程度越好。该函数以（m,b）为输入，并根据模拟数据点与直线的匹配程度返回一个误差值。为了计算给定直线的误差，我们将遍历给定模拟数据集中的每个数据点（x，y），并求出每个点的y值与候选直线y值之间的平方距离（Square Distance）之和。误差函数可定义如下：
示例代码：

def error_function(b,m,points):
    totalError=0
    for i in range(0,len(points)):
        x=points[i][0]
        y=points[i][1]
        totalError+=(y-(m*x+b))**2
    return totalError/float(len(points))

现在我们就可以进行接下来执行梯度算法，梯度下降算法实现的示例代码如下：

def step_gradient(m_current,b_current,points,learningRate):
    '''
    梯度下降算法核心方法
    参数说明
    m_current:当前斜率值m
    b_current:当前截距值b
    points:模拟数据点集合
    learningRate:学习率，也是每次移动的步长
    '''
    b_gradient=0 #erro函数关于b的偏导数
    m_gradient=0 #erro函数关于m的偏导数
    N=float(len(points)) #数据集长度
    #通过梯度下降计算更新后的m与b值
    for i in range(0,len(points)):
        x=points[i,0]
        y=points[i,1]
        #erro函数对b求偏导数
        b_gradient+=-(2/N)*x*(y-((m_current*x)+b_current))

学习率变量控制在每次迭代中“走下坡路”的幅度.为确保梯度下降正常工作的最好方式是确保每次迭代的误差持续递减。
基于上述定义的误差函数和梯度计算方法，就可以通过多次梯度下降算法来获取最佳拟合直线的斜率m和截距b。示例代码如下：

from numpy import *
def gradient_descent_runner(points,starting_b,starting_m,learning_rate,num_iterations):
    '''
    定义梯度下降运行方法
    points:模拟数据点集合
    starting_b:初始化b值
    starting_m:初始化m值
    learningRate：学习率，也是每次移动的步长
    num_iterations:迭代次数
    '''
    b=starting_b #初始化b值
    m=starting_m
    b_m_sets=[] #用于存放所有拟合直线的m，b值
    #梯度下降算法迭代
    for i in range(num_iterations):
        b,m=step_gradient(b,m,array())
        b_m_sets.append([b,m])
    #返回所有拟合直线的m，b值
    return b_m_sets
def run():
    '''
    定义主程序
    读取本地文件，设置本地曲线
    通过多次梯度下降算法迭代来获取最佳拟合直线的斜率m与截距b
    '''
    points=genfromtxt('data.csv',delimiter=',')
    learning_rate=0.0001
    initial_b=0 #初始化b值
    initial_m=0 #初始化m值
    num_iterations=100 #迭代次数
    print("Starting gradient descent at b={0},m={1},error={2}".format(initial_b,initial_m,error_function(initial_b,initial_m,points)))
    #通过梯度下降算法获取拟合直线的m，b值
    parameters=gradient_descent_runner(points,initial_b,initial_m,learning_rate,num_iterations)
    [b,m]=parameters[-1]
    print('After {0} iterations b={1},m={2},error={3}'.format(num_iterations,b,m,error_function(b,m,points)))
    # 可视化输出数据点，最佳拟合直线以及误差梯度下降曲线
    gd_visualization(points,parameters,num_iterations)
    def gd_visualization(points,parameters,iter_num):
        xx=[]
        yy=[]
        for i in range(len(points)):
            xx.append(points[i][0])
            yy.append(points[i][1])
        plt.plot(xx,yy,'bo',label='模拟数据点')
        plt.title('一元线性回归分析示例')
        plt.xlabel('x')
        plt.ylabel('y')
        plt.grid(False)
        [b,m]=parameters[-1]
        x=np.linspace(0,100,100)
        y=m*x+b
        plt.plot(x,y,'r-',label='最佳拟合直线')
        plt.legend()
        plt.show()
        erro=[]
        for j in range(len(parameters)):
            [b,m]=parameters[j]
            erro.append(error_function(b,m,points))
        iteration=range(iter_num)
        plt.plot(iteration,erro,'b--',label='误差函数梯度下降函数')
        plt.xlabel('迭代次数')
        plt.ylabel('误差')
        plt.legend()
        plt.show()
if __name__=='__main__':
    run()

算法总结

在线性回归问题中，一般只有一个极小值。我们定义的误差函数为凸曲线。因此无论从哪里开始，最终都会到达绝对最小值。一般来说，并非所有情况皆如此，有些函数可能存在局部极小值，普通的梯度下降搜索则有可能会陷入其中，而通过随机梯度下降（Stochastic Gradient Descent，SGD）算法，在某种程度上可缓解这种情况。除了设定明确的循环次数之外，我们也可通过其他方式（例如设定收敛条件等）来终止循环。当梯度小于某个设定值时，表明迭代已经接近函数极值，则退出迭代循环。