数据结构：图的遍历

图创建不懂的戳这，这节遍历是基于上节的图结构

图的遍历：从图的某个顶点出发，依次访问图中所有的顶点，每个顶点被访问一次且仅访问一次。
防止多次访问某一个顶点的思路：设置辅助数组visited[n],用来标记每个被访问的顶点，
初始化状态为visited[n]=0;如果顶点被访问到，则修改辅助数组的值 ：visited[i]=1

深度遍历DFS

• 访问顶点V
• 依次从顶点V的未被访问的邻节点出发，进行深度优先搜索，直至和V有路径相通的顶点都被访问到。
• 对于连通图进行遍历时，从一个顶点出发即可访问图中所有的顶点。
• 对于非连通图进行遍历时，若图中尚有顶点未被访问，则另选一未曾访问的顶点作为起始点，进行深度优先搜索，直至所有顶点都被访问

void Graph::DFS(char v)//深度遍历
{
	bool* visited = new bool[NumVertex];
	for (int i = 0; i < NumVertex; ++i)
	{
		visited[i] = false;
	}
	int index = GetVertexIndex(v);//获取当前顶点的下标
	DFS(index, visited);
	delete[]visited;
	visited = nullptr;
}
void Graph::DFS(int index, bool* visited)//深度遍历
{
	cout << VerArr[index].m_VertexValue << " ";  //遍历当前顶点
	visited[index] = true;//标记为tue，说明被访问了
	Edge* p = VerArr[index].m_list;
	while (p)
	{
		//从当前顶点没有被访问的领结顶点开始继续DFS
		if (!visited[p->m_destvalue])
		{
			DFS(p->m_destvalue, visited);
		}
		//如果当前顶点的邻接顶点被访问，从下一个邻接顶点开始访问
		p = p->m_next;
	}
}

广度优先BFS

类似于树的按层次遍历
1、从图中某个顶点v出发，访问v
2、依次访问v的各个未被访问过的邻接点
3、分别从这些邻接点出发依次访问他们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点” 被访问
4、重复3，直到所有已被访问的顶点的邻接点都被访问到。

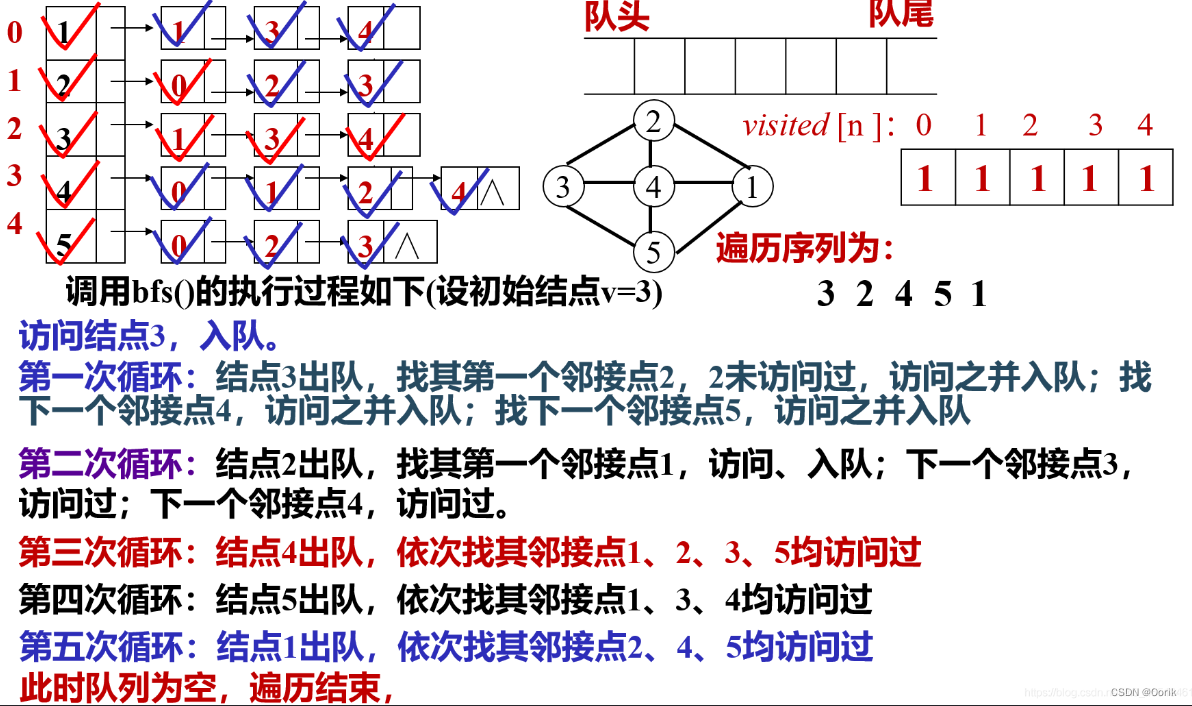
//BFS遍历，广度
void Graph::BFS(char v)
{
	//定义标记数组,标记当前顶点是否被访问
	bool* visited = new bool[NumVertex];
	for (int i = 0; i < NumVertex; ++i)
	{
		visited[i] = false;
	}
	int index = GetVertexIndex(v);//获取当前顶点的下标
	if (index == -1)return;
	queue<int>que;//定义队列存储访问顶点的下标(邻接表里存储的是下标)
	int front;//标记对头元素
	Edge* p = nullptr;//指向当前顶点的边链表
	que.push(index);//将当前顶点入队
	cout << v<< " ";//打印即是访问顶点
	visited[index] = true;
	while (!que.empty())
	{
		front = que.front();
		que.pop();
		p = VerArr[front].m_list;//p指向当前顶点的邻接表
		//开始访问front所指的顶点所有未被访问邻接顶点
		while (p != nullptr)
		{
			if (!visited[p->m_destvalue])//如果邻接顶点没访问
			{
				cout << VerArr[p->m_destvalue].m_VertexValue << " ";//把没访问的值输出
				visited[p->m_destvalue] = true;//把他置为true，说明这下访问过了
				que.push(p->m_destvalue);//把他入队
			}
			p = p->m_next;//这条邻接表查看完了，查看下一条

		}
	}
	delete[]visited;
	visited = nullptr;
}