cdq分治 学习笔记
什么是 c d q cdq cdq 分治
一种很优美的分治,具体来说,我们解决 [ l , r ] [l,r] [l,r] 这个,跟普通的分治大体思路一样,也是先分治 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d , r ] [mid,r] [mid,r],然后算答案。
大体思路
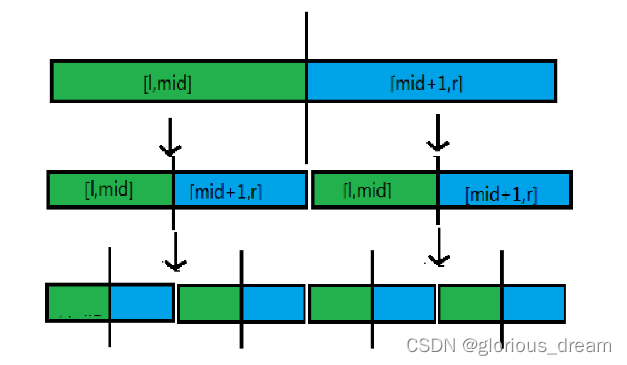
- 将一个区间 [ l , r ] [l,r] [l,r] 一直向下二分,变成 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r]
- 返回的时候,分别处理区间 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r],用双指针。具体来说,一个指针 i i i 指向 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 这个区间,一个指针 j j j 指向 [ l , m i d ] [l,mid] [l,mid] 这个区间,处理的时候以当前值作为下标,一般来说和树状数组配合使用。 ( ( (好像有点抽象 ) ) )
- 合并区间 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r],然后计算贡献。
例题
接下来以一道模板题进行讲解。
洛谷 P3810 【模板】三维偏序(陌上花开)

一道经典的三位偏序题。用
a
a
a 表示第一维,
b
b
b 表示第二维,
c
c
c 表示第三维,
c
n
t
cnt
cnt 记录个数
(
(
(题目中的要求
)
)
)。
然后我们来看怎么进行 c d q cdq cdq 分治。首先我们按第一维排序。就是下面的函数。
inline bool cmp1(node a,node b){
if(a.a == b.a){
if(a.b == b.b) return a.c < b.c;
else return a.b < b.b;
}
return a.a < b.a;
}
然后我们进行 c d q ( 1 , n ) cdq(1,n) cdq(1,n)。我们先往下进行二分,将区间 [ l , r ] [l,r] [l,r] 二分为 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r],并且在 l = r l=r l=r 的时候返回。
if(l == r) return;
int mid = (l+r)>>1;
cdq(l,mid),cdq(mid+1,r);
接下来就是处理这个区间了。我们将这两个区间分别按第二维排序。
inline bool cmp2(node a,node b){
if(a.b == b.b) return a.c < b.c;
return a.b < b.b;
}
sort(s2+l,s2+mid+1,cmp2);
sort(s2+mid+1,s2+r+1,cmp2);
这样的话,就相当于,已经保证了 [ l , m i d ] [l,mid] [l,mid] 的第一维小于 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 的第一维,并且保证了 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 内的第二维是单调不下降的。接下来我们就可以建立两个指针 i , j i,j i,j,分别指向 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 和 [ l , m i d ] [l,mid] [l,mid]。此时,对于每一个 s 2 [ i ] s2[i] s2[i] 和 s 2 [ j ] s2[j] s2[j],已经有 s 2 [ i ] s2[i] s2[i] 的第一维大于 s 2 [ j ] s2[j] s2[j] 的第一维,那么我们让 i i i 从 m i d + 1 mid+1 mid+1 循环到 r r r,一旦遇到 s 2 [ i ] . b ≥ s 2 [ j ] . b s2[i].b \geq s2[j].b s2[i].b≥s2[j].b 并且 j ≤ m i d j \leq mid j≤mid 的 j j j,我们就把 s 2 [ j ] s2[j] s2[j] 加入以 s 2 [ j ] . c s2[j].c s2[j].c 为下标, s 2 [ j ] . c n t s2[j].cnt s2[j].cnt 为权值的树状数组中吗,最后统计 s 2 [ i ] s2[i] s2[i] 的答案。就是直接 q u e r y ( s 2 [ i ] . c ) query(s2[i].c) query(s2[i].c),相当于在第一维排好序后,第二维和第三维是一个求逆序对的操作。
int j = l;
for(re int i(mid+1) ; i<=r ; ++i){
while(s2[i].b >= s2[j].b && j <= mid){
add(s2[j].c,s2[j].cnt);
j++;
}
s2[i].ans += query(s2[i].c);
}
最后别忘了要清空树状数组,因为每一层是互相独立的。
rep(i,l,j-1) add(s2[i].c,-s2[i].cnt);
以上就是 c d q cdq cdq 分治的操作。统计答案的时候,对于这道题来说, s 2 [ i ] s2[i] s2[i] 的答案就是比 s 2 [ i ] s2[i] s2[i] 小的元素加上 s 2 [ i ] s2[i] s2[i] 的元素个数减 1 1 1。
最后放上总代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#define re register
#define drep(a,b,c) for(re int a(b) ; a>=(c) ; --a)
#define rep(a,b,c) for(re int a(b) ; a<=(c) ; ++a)
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
inline void print(int x){
if(x < 0) putchar('-'),x = -x;
if(x >= 10) print(x / 10);
putchar(x % 10 + '0');
}
const int M = 2e5+10;
int n,k,m,cnt;
int res[M],c[M];
struct node{
int a,b,c,cnt,ans;
}s1[M],s2[M];
inline bool cmp1(node a,node b){
if(a.a == b.a){
if(a.b == b.b) return a.c < b.c;
else return a.b < b.b;
}
return a.a < b.a;
}
inline bool cmp2(node a,node b){
if(a.b == b.b) return a.c < b.c;
return a.b < b.b;
}
inline int lowbit(int x) { return x&-x; }
inline void add(int x,int y){
while(x <= k){
c[x] += y;
x += lowbit(x);
}
}
inline int query(int x){
int res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
inline void cdq(int l,int r){
if(l == r) return;
int mid = (l+r)>>1;
cdq(l,mid),cdq(mid+1,r);
sort(s2+l,s2+mid+1,cmp2);
sort(s2+mid+1,s2+r+1,cmp2);
int j = l;
for(re int i(mid+1) ; i<=r ; ++i){
while(s2[i].b >= s2[j].b && j <= mid){
add(s2[j].c,s2[j].cnt);
j++;
}
s2[i].ans += query(s2[i].c);
}
rep(i,l,j-1) add(s2[i].c,-s2[i].cnt);
}
signed main(){
n = read(),k = read();
rep(i,1,n) scanf("%d%d%d",&s1[i].a,&s1[i].b,&s1[i].c);
sort(s1+1,s1+n+1,cmp1);
rep(i,1,n){
cnt++;
if(s1[i].a != s1[i+1].a || s1[i].b != s1[i+1].b || s1[i].c != s1[i+1].c){
m++;
s2[m] = s1[i];
s2[m].cnt = cnt;
cnt = 0;
}
}
cdq(1,m);
rep(i,1,m) res[s2[i].ans+s2[i].cnt-1] += s2[i].cnt;
rep(i,0,n-1) printf("%d\n",res[i]);
return 0;
}
洛谷 P3157 [CQOI2011]动态逆序对

也是一道板子题,用两次
c
d
q
cdq
cdq 分治。我们反过来想,每次考虑当前数字被删除之后会减少多少个逆序对。对于每一个数字,删除之后减少的逆序对个数,即为它对于全局的贡献。是:
- 在它之前且比它大 / / / 在它之后且比它小
- 删除时间比它晚。
对于没有删除的元素,我们把删除的时间赋值为无穷大,然后就是正常的三维偏序了。
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#define re register
#define drep(a,b,c) for(re int a(b) ; a>=(c) ; --a)
#define rep(a,b,c) for(re int a(b) ; a<=(c) ; ++a)
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
inline void print(int x){
if(x < 0) putchar('-'),x = -x;
if(x >= 10) print(x / 10);
putchar(x % 10 + '0');
}
const int M = 2e5+10;
int n,m,cnt;
int id[M],res[M],a[M],c[M],ans[M];
struct node{
int id,tim,val;
}s[M];
inline bool cmp1(node a,node b) { return a.tim > b.tim; }
inline bool cmp2(node a,node b){
if(a.id == b.id) return a.val > b.val;
return a.id < b.id;
}
inline bool cmp3(node a,node b){
if(a.id == b.id) return a.val < b.val;
return a.id > b.id;
}
inline int lowbit(int x) { return x&-x; }
inline void update(int x,int y){
while(x <= n){
c[x] += y;
x += lowbit(x);
}
}
inline int query(int x){
int res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
inline int work(){
int res = 0;
rep(i,1,n){
update(a[i],1);
res += (i-query(a[i]));
}
memset(c,0,sizeof(c));
return res;
}
inline void cdq1(int l,int r){ //前,大
if(l == r) return;
int mid = (l+r)>>1;
cdq1(l,mid),cdq1(mid+1,r);
sort(s+l,s+mid+1,cmp2);
sort(s+mid+1,s+r+1,cmp2);
int j = l;
for(re int i(mid+1) ; i<=r ; ++i){
while(j <= mid && s[j].id < s[i].id){
update(s[j].val,1);
j++;
}
ans[s[i].tim] += query(n) - query(s[i].val);
}
rep(i,l,j-1) update(s[i].val,-1);
}
inline void cdq2(int l,int r){ //后,小
if(l == r) return;
int mid = (l+r)>>1;
cdq2(l,mid),cdq2(mid+1,r);
sort(s+l,s+mid+1,cmp3);
sort(s+mid+1,s+r+1,cmp3);
int j = l;
for(re int i(mid+1) ; i<=r ; ++i){
while(j <= mid && s[j].id > s[i].id){
update(s[j].val,1);
j++;
}
ans[s[i].tim] += query(s[i].val);
}
rep(i,l,j-1) update(s[i].val,-1);
}
signed main(){
n = read(),m = read();
rep(i,1,n){
int x = read();
id[x] = i;
a[i] = x;
s[++cnt] = (node){i,200000,x};
}
rep(i,1,m){
int x = read();
s[id[x]].tim = i;
}
ans[0] = work();
sort(s+1,s+cnt+1,cmp1);
cdq1(1,cnt);
sort(s+1,s+cnt+1,cmp1);
cdq2(1,cnt);
printf("%lld\n",ans[0]);
rep(i,1,m-1){
ans[i] = ans[i-1] - ans[i];
printf("%lld\n",ans[i]);
}
return 0;
}
洛谷 P4169 [Violet]天使玩偶/SJY摆棋子

这道题的处理很神仙。由于有绝对值,我们直接处理不好处理,那么我们考虑如何去掉绝对值。那么显然,对于一个点
(
x
,
y
)
(x,y)
(x,y),每一个在它左下角的点,可以直接把绝对值给去掉。那么我们考虑进行旋转,也就是转三次,将每个点都能转到该点的下方,这样的话最后答案一定就是正确的。我们记录一下操作的
o
p
op
op,等于
1
1
1 是回忆点,等于
2
2
2 是询问。每次
c
d
q
cdq
cdq 的时候,对于两个区间
[
l
,
m
i
d
]
[l,mid]
[l,mid] 和
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r],
[
l
,
m
i
d
]
[l,mid]
[l,mid] 这个区间能对
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r] 产生贡献的,就是在
[
l
,
m
i
d
]
[l,mid]
[l,mid] 里面,并且
o
p
=
1
op=1
op=1 表示这是回忆起来的坐标。我们把
b
[
t
1
]
.
x
+
b
[
t
1
]
.
y
b[t1].x+b[t1].y
b[t1].x+b[t1].y 插入以
b
[
t
1
]
.
x
b[t1].x
b[t1].x 为下标的树状数组中,在查询答案的时候,我们取
b
[
t
2
]
.
x
+
b
[
t
2
]
.
y
−
q
u
e
r
y
(
b
[
t
2
]
.
y
)
b[t2].x+b[t2].y-query(b[t2].y)
b[t2].x+b[t2].y−query(b[t2].y) 的最小值。因为
q
u
e
r
y
query
query 就是上面那个式子,相减就是把绝对值给去掉了。像这样进行四次取
min
\min
min 即可。
注意,这题坑点挺多的。首先不能在 c d q cdq cdq 的过程中 s o r t sort sort,应该在处理的时候同时进行归并排序。而且,树状数组下标不能从 0 0 0 开始,我们把每一个 x x x 和 y y y 都加 1 1 1 就行。注意,一开始树状数组要赋值为负无穷,然后每次往下取 max \max max。
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define re register
#define rep(a,b,c) for(re int a(b) ; a<=c ; ++a)
#define drep(a,b,c) for(re int a(b) ; a>=c ; --a)
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
return x*f;
}
const int M = 1e7+10;
const int inf = 2e9;
int n,q,len;
struct node{
int op,id,x,y,ans;
}a[M],b[M],tmp[M];
int c[M];
inline int lowbit(int x) { return x & -x; }
inline void update(int x,int y){
while(x <= len){
c[x] = max(c[x],y);
x += lowbit(x);
}
}
inline int query(int x){
int res = -inf;
while(x){
res = max(res,c[x]);
x -= lowbit(x);
}
return res;
}
inline void clear(int x){
while(x <= len){
c[x] = -inf;
x += lowbit(x);
}
}
inline void cdq(int l,int r){
if(l == r) return;
int mid = (l+r)>>1;
cdq(l,mid),cdq(mid+1,r);
int t1 = l,t2 = mid+1;
int k = l;
while(t2 <= r){
while(t1 <= mid && b[t1].x <= b[t2].x){
if(b[t1].op == 1) update(b[t1].y,b[t1].x+b[t1].y);
tmp[k++] = b[t1++];
}
if(b[t2].op == 2) a[b[t2].id].ans = min(a[b[t2].id].ans,b[t2].x+b[t2].y-query(b[t2].y));
tmp[k++] = b[t2++];
}
rep(i,l,t1-1) if(b[i].op == 1) clear(b[i].y);
while(t1 <= mid) tmp[k++] = b[t1++];
rep(i,l,r) b[i] = tmp[i];
}
inline void solve(int px,int py){
rep(i,1,n+q){
b[i] = a[i];
if(px) b[i].x = len - b[i].x;
if(py) b[i].y = len - b[i].y;
}
cdq(1,n+q);
}
signed main(){
n = read(),q = read();
rep(i,0,M-1) c[i] = -inf;
rep(i,1,n){
int x = read() + 1,y = read() + 1;
a[i].op = 1;
a[i].id = i;
a[i].x = x;
a[i].y = y;
len = max({len,x,y});
}
rep(i,n+1,n+q){
int op = read(),x = read() + 1,y = read() + 1;
a[i].op = op;
a[i].id = i;
a[i].x = x;
a[i].y = y;
a[i].ans = inf;
len = max({len,x,y});
}
len++;
solve(0,0),solve(0,1),solve(1,0),solve(1,1);
rep(i,n+1,n+q) if(a[i].op == 2) printf("%d\n",a[i].ans);
return 0;
}
洛谷 P3658 [USACO17FEB]Why Did the Cow Cross the Road III P

记录一下自己用了独特的两个树状数组解法。
我们开一个结构体,记录三个东西 u p , d o w n , v a l up,down,val up,down,val,分别表示这个数 v a l val val 在 A A A 排列中的位置,在 B B B 排列中的位置,这个数的值 ( ( (也就是 v a l ) val) val)。然后我们发现,这道题就变成了一道三位偏序的问题。我们可以先按 u p up up 从小到大排序。如果要满足对应的线交叉,那么对于两个数 x , y x,y x,y,如果在 A A A 中 x x x 在 y y y 前面,那么在 B B B 中 x x x 就必须在 y y y 后面。那么由于第一维是从小到大排序的,第二维我们就要从大到小排序。还是分成两个区间 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r],分别从大到小排序。
考虑如何算贡献。我们记 i i i 指向 [ m i d + 1 , r ] [mid+1,r] [mid+1,r], j j j 指向 [ l , m i d ] [l,mid] [l,mid],那么当 a [ j ] . d o w n > a [ i ] . d o w n a[j].down > a[i].down a[j].down>a[i].down 的时候,第二维的偏序也满足关系了。这时我们就要考虑怎么把式子给拆开。
∣ i − j ∣ > k ⇒ i − j > k 或 i − j < − k ⇒ i > j + k 或 i < j − k | i-j | > k \Rightarrow i-j>k 或 i-j<-k \Rightarrow i>j+k 或 i<j-k ∣i−j∣>k⇒i−j>k或i−j<−k⇒i>j+k或i<j−k
那么我们开两个树状数组,一个往上维护,一个往下维护。在 j j j 满足条件的时候,我们分别在两个树状数组中, a [ j ] . v a l a[j].val a[j].val 为下标的地方 + 1 +1 +1。然后我们统计答案的时候,一个我们 q u e r y 1 ( a [ i ] . v a l − k − 1 ) query1(a[i].val-k-1) query1(a[i].val−k−1),一个 q u e r y 2 ( a [ i ] . v a l + k + 1 ) query2(a[i].val+k+1) query2(a[i].val+k+1),这两个的和就是答案。
注意,两个树状数组,由于维护的方向正好是相反的,所以我们要开两个数组。我一开始就开了一个数组,然后改了好长时间。
#include <bits/stdc++.h>
#define re register
#define ll long long
#define int long long
#define rep(a,b,c) for(re int a(b) ; a<=c ; ++a)
#define drep(a,b,c) for(re int a(b) ; a>=c ; --a)
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
return x*f;
}
const int M = 2e5+10;
int n,k,ans;
int c1[M],c2[M];
struct node{
int up,down,val;
}a[M];
inline int lowbit(int x) { return x & -x; }
inline void update1(int x,int y){
while(x <= n){
c1[x] += y;
x += lowbit(x);
}
}
inline void update2(int x,int y){
while(x){
c2[x] += y;
x -= lowbit(x);
}
}
inline int query1(int x){
if(x < 1) return 0;
int res = 0;
while(x){
res += c1[x];
x -= lowbit(x);
}
return res;
}
inline int query2(int x){
if(x > n) return 0;
int res = 0;
while(x <= n){
res += c2[x];
x += lowbit(x);
}
return res;
}
inline bool cmp1(node a,node b) { return a.up < b.up; }
inline bool cmp2(node a,node b) { return a.down > b.down; }
inline void cdq(int l,int r){
if(l == r) return;
int mid = (l+r)>>1;
cdq(l,mid),cdq(mid+1,r);
sort(a+l,a+mid+1,cmp2),sort(a+mid+1,a+r+1,cmp2);
int j = l;
rep(i,mid+1,r){
while(j <= mid && a[j].down > a[i].down){
update1(a[j].val,1);
update2(a[j].val,1);
j++;
}
ans += query1(a[i].val-k-1) + query2(a[i].val+k+1);
}
rep(k,l,j-1) update1(a[k].val,-1),update2(a[k].val,-1);
}
signed main(){
n = read(),k = read();
rep(i,1,n){
int x = read();
a[x].up = i;
a[x].val = x;
}
rep(i,1,n){
int x = read();
a[x].down = i;
}
sort(a+1,a+n+1,cmp1);
cdq(1,n);
printf("%lld\n",ans);
return 0;
}
洛谷 P4390 [BOI2007]Mokia 摩基亚

我们先来考虑如何进行二维数点。对于区间
[
x
1
,
y
1
]
[
x
2
,
y
2
]
[x1,y1][x2,y2]
[x1,y1][x2,y2],我们转化为
(
1
,
1
)
(
x
1
−
1
,
y
1
−
1
)
+
(
1
,
1
)
(
x
2
,
y
2
)
−
(
1
,
1
)
(
x
1
−
1
,
y
2
)
−
(
1
,
1
)
(
x
2
,
y
1
−
1
)
(1,1)(x1-1,y1-1)+(1,1)(x2,y2)-(1,1)(x1-1,y2)-(1,1)(x2,y1-1)
(1,1)(x1−1,y1−1)+(1,1)(x2,y2)−(1,1)(x1−1,y2)−(1,1)(x2,y1−1),即拆为
4
4
4 个询问用树状数组求即可。
那么这道题,我们把时间看成一维, x x x 和 y y y 分别看成一维,就变成了一个三维偏序的模板题了。也就是我们要求 t i m e a < t i m e b timea < timeb timea<timeb, x a < x b xa<xb xa<xb, y a < y b ya<yb ya<yb 的数量。最后我们将询问的输出重新按顺序排序,接着按上面的容斥输出答案即可。同样需要注意,树状数组的下标不能为 0 0 0,所以我们把每一个 x x x 和 y y y 都加一就行。
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define re register
#define rep(a,b,c) for(re int a(b) ; a<=c ; ++a)
#define drep(a,b,c) for(re int a(b) ; a>=c ; --a)
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
return x*f;
}
const int M = 2e6+10;
int n,op,cnt;
int c[M];
struct node{
int x,y,w,id,tim;
}a[M];
inline int lowbit(int x) { return x & -x; }
inline void update(int x,int y){
while(x <= n){
c[x] += y;
x += lowbit(x);
}
}
inline int query(int x){
int res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
inline bool cmp(node a,node b){
if(a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
inline void cdq(int l,int r){
if(l == r) return;
int mid = (l+r)>>1;
cdq(l,mid),cdq(mid+1,r);
sort(a+l,a+mid+1,cmp),sort(a+mid+1,a+r+1,cmp);
int j = l;
rep(i,mid+1,r){
while(j <= mid && a[j].x <= a[i].x){
if(a[j].id == 0) update(a[j].y,a[j].w);
j++;
}
if(a[i].id == 1) a[i].w += query(a[i].y);
}
rep(k,l,j-1) if(a[k].id == 0) update(a[k].y,-a[k].w);
}
inline bool cmp2(node a,node b) { return a.tim < b.tim; }
signed main(){
read(),n = read() + 1;
while(scanf("%d",&op)){
if(op == 3) break;
if(op == 1){
int x = read() + 1,y = read() + 1,w = read();
a[++cnt] = (node){x,y,w,0,cnt};
}
else{
int x1 = read() + 1,y1 = read() + 1,x2 = read() + 1,y2 = read() + 1;
a[++cnt] = (node){x2,y2,0,1,cnt};
a[++cnt] = (node){x2,y1-1,0,1,cnt};
a[++cnt] = (node){x1-1,y2,0,1,cnt};
a[++cnt] = (node){x1-1,y1-1,0,1,cnt};
}
}
cdq(1,cnt);
sort(a+1,a+cnt+1,cmp2);
rep(i,1,cnt){
if(a[i].id == 1){
printf("%d\n",a[i].w-a[i+1].w-a[i+2].w+a[i+3].w);
i += 3;
}
}
return 0;
}
CF1045G AI robots

这道题的
k
k
k 的范围是
0
≤
k
≤
20
0 \leq k \leq 20
0≤k≤20,所以我们可以双指针扫。
具体来说,我们先对于位置离散化,把每一个点所能看到的区间 [ l , r ] [l,r] [l,r] 给记录下来。我们把 x i x_i xi 这一维离散化,然后在离散化的数组中找 x [ i ] − r [ i ] x[i]-r[i] x[i]−r[i] 和 x [ i ] + r [ i ] x[i]+r[i] x[i]+r[i] 的位置,这就是这个点能看到的范围 [ l , r ] [l,r] [l,r],同时还要把 x i x_i xi 这一维给离散化。然后我们就得到了每一个点能看到的区间,我们进行 c d q cdq cdq 分治。
k k k 是固定的,我们左右两个区间 [ l , m i d ] [l,mid] [l,mid] 和 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 按智商排序,然后双指针扫对于每一个在 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 中的点,哪些点可以对它产生贡献,就是智商之差 ≤ k \leq k ≤k 的在 [ l , m i d ] [l,mid] [l,mid] 中的点。同时这是有单调性的,所以我们可以双指针扫,然后加入树状数组中统计答案,最后别忘了删除,就跟普通的模板类似了。
#include <bits/stdc++.h>
#define re register
#define ll long long
#define rep(a,b,c) for(re int a(b) ; a<=c ; ++a)
#define drep(a,b,c) for(re int a(b) ; a>=c ; --a)
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
return x*f;
}
const int M = 2e5+10;
int n,k;
ll ans;
struct node{
int x,len,q,l,r;
}a[M];
int lsh[M],c[M];
inline int lowbit(int x) { return x & -x; }
inline void update(int x,int y){
while(x <= n){
c[x] += y;
x += lowbit(x);
}
}
inline int query(int x){
int res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
inline bool cmp1(node a,node b) { return a.len > b.len; }
inline bool cmp2(node a,node b) { return a.q < b.q; }
inline void cdq(int l,int r){
if(l == r) return;
int mid = (l+r)>>1;
cdq(l,mid),cdq(mid+1,r);
sort(a+l,a+mid+1,cmp2),sort(a+mid+1,a+r+1,cmp2);
int L = l,R = l-1;
rep(i,mid+1,r){
while(L <= mid && a[i].q-a[L].q > k) update(a[L].x,-1),L++;
while(R < mid && a[R+1].q-a[i].q <= k) R++,update(a[R].x,1);
ans += query(a[i].r) - query(a[i].l-1);
}
rep(i,L,R) update(a[i].x,-1);
}
signed main(){
n = read(),k = read();
rep(i,1,n){
scanf("%d%d%d",&a[i].x,&a[i].len,&a[i].q);
lsh[i] = a[i].x;
}
sort(lsh+1,lsh+n+1);
int tot = unique(lsh+1,lsh+n+1)-lsh-1;
rep(i,1,n){
a[i].l = lower_bound(lsh+1,lsh+tot+1,a[i].x-a[i].len)-lsh;
a[i].r = upper_bound(lsh+1,lsh+tot+1,a[i].x+a[i].len)-lsh-1;
a[i].x = lower_bound(lsh+1,lsh+tot+1,a[i].x)-lsh;
}
sort(a+1,a+n+1,cmp1);
cdq(1,n);
printf("%lld\n",ans);
return 0;
}
